Qual afirmação a respeito de um sistema de cargas puntiformes fixas no espaço é necessariamente verdadeira?
Se a energia potencial do sistema é negativa, um agente externo tem de realizar um trabalho positivo pra levar as cargas do sistema de volta para o infinito;
Se a energia potencial do sistema é negativa, um agente externo tem de realizar um trabalho positivo pra agrupar o sistema de cargas;
Se a energia potencial do sistema é zero, não há cargas negativas no sistema;
Se a energia potencial do sistema é positiva, requer-se um trabalho total positivo para trazer qualquer nova carga do infinito para sua posição final no sistema;
Se a energia potencial do sistema é positiva, um agente externo tem de realizar um trabalho positivo pra levar as cargas do sistema de volta para o infinito;
Passo 1
Então vamos analisar cada opção aqui, beleza?
Se a energia potencial do sistema é negativa, um agente externo tem de realizar um trabalho positivo pra levar as cargas do sistema de volta para o infinito;
Nessa situação o ponto inicial é o sistema, que possui energia potencial negativa , e o ponto final é o infinito, que possui energia potencial nula , logo:
Ou seja, nesse caso, uma força externa precisa adicionar uma energia para levar as cargas até o infinito, assim o trabalho da força externa é positivo sim!
Repara que o trabalho da força externa é diferente do trabalho da força elétrica. O trabalho da força elétrica é dado por .
Essa é a frase correta, mas vamos dar uma olhadinha nas outras opções pra mandar bem! ;)
Passo 2
Se a energia potencial do sistema é negativa, um agente externo tem de realizar um trabalho positivo pra agrupar o sistema de cargas;
Agora o ponto inicial é o infinito e o ponto final é o sistema com energia potencial negativa , logo
O trabalho da força externa dessa vez é negativo (diferente do trabalho da força elétrica que é positivo), assim essa opção está errada.
Passo 3
Se a energia potencial do sistema é zero, não há cargas negativas no sistema;
Se pensarmos numa configuração de cargas que tem energia potencial total nula provamos que essa afirmação está errada.
O mais simples que eu consigo pensar é isso aqui, ó
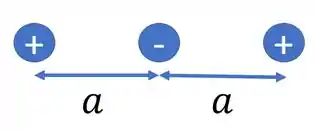
Se a carga do meio for e as das pontas forem então a energia potencial do sistema será
E pra isso ser basta que
Assim conseguimos pensar num sistema de cargas com uma carga no sistema, logo a frase é falsa.
Passo 4
Se a energia potencial do sistema é positiva, requer-se um trabalho total positivo para trazer qualquer nova carga do infinito para sua posição final no sistema;
Nesse caso o ponto inicial é o infinito e o ponto final é o sistema com energia potencial positiva , logo:
O trabalho da força externa é dado por
Já o trabalho da força elétrica é dado por
Assim o trabalho total é dado por
Logo, a letra D também está errada.
Passo 5
Se a energia potencial do sistema é positiva, um agente externo tem de realizar um trabalho positivo pra levar as cargas do sistema de volta para o infinito;
Aqui o ponto inicial é o sistema com energia potencial positiva e o ponto final é o infinito , logo:
O trabalho de uma força externa então seria dado por
Assim a frase está errada.