Três cargas puntiformes, inicialmente muito afastadas entre si, estão sobre os vértices de um triângulo equilátero, de lado igual a . Duas dessas cargas são idênticas e possuem carga . Desejamos realizar um trabalho líquido igual a zero para colocar as três cargas nos vértices do triângulo; qual deve ser o valor da terceira carga?
Passo 1
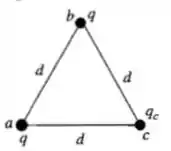
Vamos começar imaginando dois casos: caso 1, quando as cargas estão infinitamente distantes; e caso 2, quando elas estão nos vértices do triângulo, como na figura abaixo. Chamamos a terceira carga, que ainda não conhecemos, de .
Passo 2
Agora, calculamos o trabalho realizado para que as cargas venham do infinito (caso 1) para os vértices do triângulos (caso 2). Temos que:
Sabemos que, para o caso 1, com as cargas no infinito, . Já para o caso 2, temos que:
Como queremos que , logo:
Logo, o valor pode ser calculado como:
Resposta
(a) .