Um elétron se move do ponto para o ponto , na direção de um campo elétrico uniforme. Durante este trajeto:

(a) o trabalho realizado pelo campo é positivo e a energia potencial do sistema campo-elétron aumenta.
(b) o trabalho realizado pelo campo é positivo e a energia potencial do sistema campo-elétron diminui.
(c) o trabalho realizado pelo campo é negativo e a energia potencial do sistema campo-elétron diminui.
(d) o trabalho realizado pelo campo é negativo e a energia potencial do sistema campo-elétron aumenta.
(e) o trabalho realizado pelo campo é positivo e a energia potencial do sistema campo-elétron não muda.
Passo 1
Primeiramente, vamos lembrar a definição de trabalho.
Considere um corpo que, pela ação de uma força vai de um ponto até o ponto , como na figura abaixo.
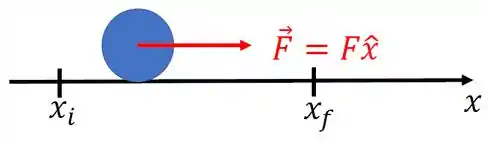
A força está na mesma direção do eixo e é constante ao longo de todo o caminho. Sendo assim, o trabalho da força para levar o corpo de até é
com . Em nosso sistema de coordenada, . Logo, . Assim, o sinal do trabalho depende do sinal de .Podemos determinar o trabalho também a partir da variação de energia potencial eletrostática do sistema. A fórmula é
sendo e , isto é, a energia potencial eletrostática calculada nas posições e .
Com essas expressões em mente, vamos resolver essa questão no próximo passo.
Passo 2
O enunciado diz que se trata de um elétron (de carga , ) imerso em uma região em que o campo elétrico é constante.
A força que o elétron sofre tem sentido contrário ao campo elétrico pois o elétron tem carga negativa. Veja a figura abaixo.
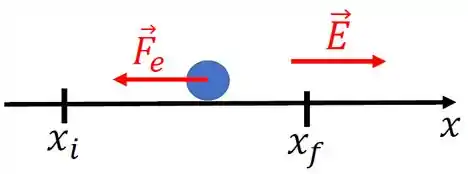
Em nosso sistema de coordenadas, a força elétrica que o elétron sofre é dada por
Portando, o trabalho da força elétrica sobre o elétron é dado por
com .
Tanto , quanto e são positivos. Com isso, concluímos que o trabalho é negativo.
OBSERVAÇÃO: Se tivéssemos o eixo no sentido contrário, obteríamos que e a força seria . Assim, , pois .
Vamos para o próximo passo!
Passo 3
Comentamos no passo 1 que o trabalho pode ser calculado por
com e as energia potenciais eletrostáticas calculadas nas posições e , respectivamente.
Como mostrado no item anterior, o trabalho da força elétrica . Assim, temos que
Como comentado, tanto , quanto e são positivos. Com isso, concluímos que a variação de energia potencial eletrostática é positiva.
Sabendo que , temos finalmente que
isto é, a energia potencial eletrostática do sistema aumentou quando o elétron foi de para .
Portanto, analisando as alternativas, vemos que a alternativa correta é a letra .