Considere os seguintes três campos vetoriais em certas regiões do espaço (as setas representam os campos, em diferentes pontos, e as curvas tracejadas, suas correspondentes linhas de campo)
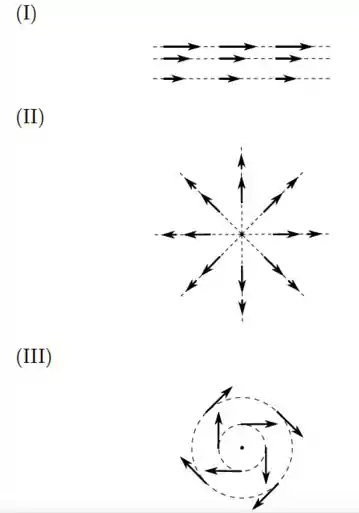
Indique a opção que melhor assinala, desses campos, aquele(s) que, de fato, não pode(m) ser campo(s) eletrostático(s). [Sugestão: um campo eletrostático tem de ser conservativo].
- Nenhum deles.
Passo 1
I) Na figura abaixo, vemos que o campo elétrico é paralelo às linhas de força e que sua intensidade varia dentro da região, pois os “tamanhos dos vetores diminuem”, o que também fica claro através do nítido “distanciamento entre as linhas de campo (tracejadas)”.
Agora, para vermos se este campo é conservativo ou não, podemos traçar as linhas em vermelho perpendiculares às linhas de campo. Os pontos e em cada linha de campo estão à mesma distância um do outro.
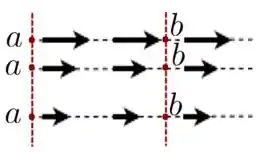
Imagina uma carga dentro desse campo da figura acima. O trabalho realizado para levar do ponto até o ponto depende da linha de campo em que esta carga está sendo transportada. Apesar de a distância entre e ser a mesma em qualquer linha, a intensidade do campo é diferente em cada uma delas. Isso significa que o trabalho realizado pelo campo sobre a carga depende da trajetória que a carga percorrerá dentro do campo e não apenas dos pontos inicial e final da partícula.
Por isso, este campo vetorial da figura acima não pode ser conservativo, pois o trabalho realizado pelo campo sobre uma partícula carregada vai depender da trajetória seguida pela carga.
Passo 2
II) A figura abaixo pode representar, por exemplo, um campo elétrico produzido por uma carga pontual positiva localizada em seu. Repare que a direção do campo elétrico coincide com a direção das linhas de campo e a intensidade desse campo diminui à medida que a distância ao centro aumenta, o que poderia caracterizar um campo “coulombiano”, que decresce com o inverso do quadrado da distância, ou seja, depende de .
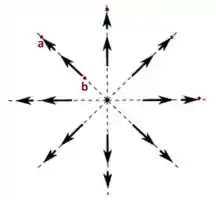
O campo coulombiano, ou campo eletrostático, é um exemplo de campo conservativo.
No entanto, a intensidade do campo nesta figura decresce com a distância ao centro do desenho (observe o tamanho dos vetores), mas não sabemos se depende de , de , etc. No entanto, todos esses campos que dependem apenas da distância radial são conservativos. Por isso, esta figura poderia representar um campo conservativo.
Passo 3
III) Nesta figura, o campo elétrico é sempre tangencial às linhas de campo. Além disso, possui a mesma intensidade em cada ponto sobre o círculo fechado da linha de campo.
Suponha que tenhamos um carga sobre o ponto indicado na figura e queiramos calcular qual o trabalho realizado por este campo para fazê-la realizar uma volta completa em cima dessa curva, ou seja, qual trabalho que o campo realiza para fazer a carga sair de e voltar para .
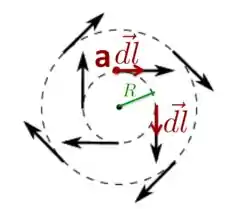
Bom, sabemos que o trabalho sobre pode ser escrito como
em que é a força sobre a carga e é curva fechada em que a carga estará durante o percurso. Podemos tomar o sentido de como sendo horário e, então, será paralelo ao campo em todo os pontos de , como mostrado na figura, e teremos: .
Como o campo elétrico é o mesmo em todos os pontos de , podemos retirar de dentro da integral e obter que:
Disso, concluímos que o trabalho realizado pelo campo sobre a carga para que ela saia de ponto e retorne a este mesmo ponto é diferente de zero! Por isso, este campo elétrico representado pela figura acima NÃO PODE SER CONSERVATIVO!
Resposta
Portanto, a resposta é a letra e).