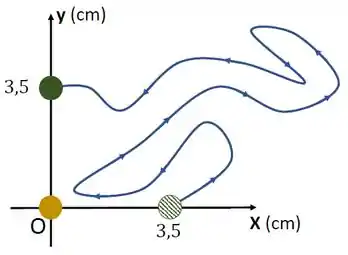
Uma partícula com uma carga de é fixada na origem. Uma segunda partícula com uma carga de é movida de no eixo para no eixo , como na figura abaixo. A mudança na energia potencial do sistema deste sistema de duas cargas é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos lembrar da energia potencial eletrostática entre duas cargas pontuais.
Dada duas cargas e , separadas por uma distância , a energia potencial dessas duas cargas é dada por
sendo .
Assim, se em uma situação inicial a distância entre as cargas é e na situação final é , então a variação de energia potencial eletrostática é dada por
Note que essa expressão não depende do caminho que as cargas fizeram: depende apenas da distância entre elas no início e no fim do movimento.
Assim, para determinar , precisamos saber primeiramente as distâncias inicial e final de nossas cargas. Veremos isso no passo 2.
Passo 2
Pela figura do enunciado, vemos imediatamente que
Olha só que maravilha!! Como , temos de imediato que
Assim, a variação de energia potencial eletrostática é nula!Na verdade isso era de se esperar. Isto porque a posição inicial e final da segunda partícula estão sobre a mesma equipotencial da primeira partícula, que está fixa na origem. Veja a figura abaixo.
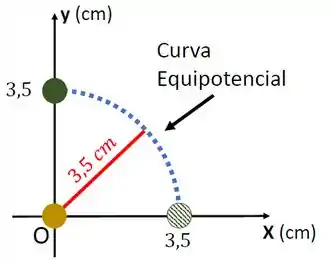
Assim, o trabalho para levar a segunda carga da posição inicial até a final seria nulo, isto é, . Como , então .
Portanto, analisando as alternativas, vemos que a alternativa correta é a letra