UFF - Física 2 – P2 2018.1 - 19
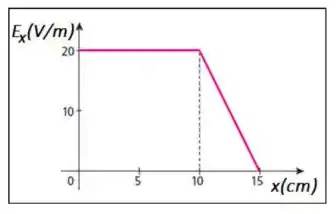
O gráfico abaixo representa , que é o componente do campo elétrico, versus a posição ao longo do eixo . Determine o valor do potencial , considerando que .
Passo 1
Primeiro, vamos precisar da expressão aqui da diferença de potencial entre dois pontos e quaisquer:
Como no problema temos apenas a componente do campo elétrico em função da distância , temos que o produto escalar da expressão acima se resume a: .
Vamos ver, agora, como fica essa diferença de potencial entres os pontos e . Do gráfico, vemos entre esses dois pontos o campo elétrico temo mesmo valor de .
Jogando isso na integral acima, teremos:
É importante lembrar aqui que o lado direito dessa igualdade é exatamente igual a área do retângulo da gráfico, de base () e altura de . Por isso, o valor dessa área é:
Como o problema diz que , tiramos que o potencial no ponto será:
Vamos utilizar esse resultado no próximo passo.
Passo 2
O potencial entre os pontos e é:
sendo que o lado direito dessa equação é igual a área embaixo da curva, ou seja, a área do triângulo do gráfico, cujo valor é:
Utilizando o resultado do Passo 1, , temos
que é o resultado que queríamos encontrar. =)
Resposta
Letra b.