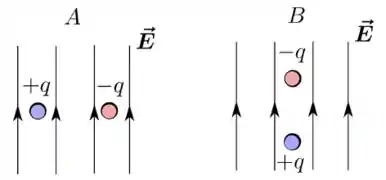
Um dipolo elétrico, formado por duas partículas de cargas e , encontra-se imerso em uma região de campo elétrico constante . Duas possíveis configurações para o dipolo, designadas por e , são mostradas na figura abaixo. Sobre essas configurações, podemos afirmar que:
- A energia potencial eletrostática do dipolo na configuração é maior do que na configuração .
- O torque que a força eletrostática exerce sobre o dipolo na configuração é nulo.
- A força resultante sobre o dipolo na configuração é mais intensa do que na configuração .
- Na configuração , o dipolo encontra-se em equilíbrio estável.
- Na configuração , o dipolo encontra-se em equilíbrio instável.
Passo 1
O vetor momento de dipolo elétrico é sempre orientado partindo da carga negativa e chegando na carga positiva . Por isso, na situação , aponta da direita para a esquerda e faz um ângulo de com o campo elétrico que é uniforme na região.
Já na situação , aponta de cima para baixo, fazendo um ângulo de com o vetor , isto é, e são anti-paralelos.
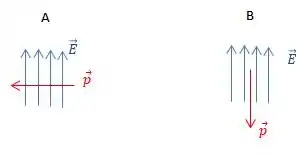
Em todas as duas configurações, a força resultante sobre o dipolo é nula, como mostra a Figura abaixo.
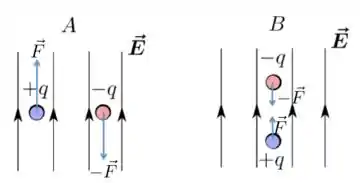
Apesar de a força resultante ser nula, o torque resultante pode ser diferente de zero. Vamos olhar com mais calma isso daqui há pouco...
Passo 2
Sabemos que o torque que um uniforme exerce sobre tem expressão dada por
O módulo de um produto vetorial é sempre dado por
em que é o ângulo entre os vetores e . Portanto, o módulo do torque é
A energia eletrostática da interação entre e é dada por
em que é o ângulo entre e e utilizamos que o produto escalar entre dois vetores e quaisquer é . Precisamos analisar como ficam essas duas expressões para as situações e do problema.
Passo 3
Situação A: Nessa configuração, o momento de dipolo elétrico está perpendicular à . Portanto, e . Portanto, o módulo do torque e a energia serão, respectivamente, iguais a
Passo 4
Situação B: Nessa configuração, o momento de dipolo elétrico está anti-paralelo a . Portanto, e . Portanto, o módulo do torque e a energia serão, respectivamente, iguais a
Essa situação é chamada de equilíbrio instável. O equilíbrio só seria estável se fosse paralelo à . Portanto, nem nem representam um equilíbrio estável!
Passo 5
Vamos agora olhar para cada alternativa:
- A energia potencial eletrostática do dipolo na configuração é maior do que na configuração .
- O torque que a força eletrostática exerce sobre o dipolo na configuração é nulo.
- A força resultante sobre o dipolo na configuração é mais intensa do que na configuração .
- Na configuração , o dipolo encontra-se em equilíbrio estável.
- Na configuração , o dipolo encontra-se em equilíbrio instável.
Vimos que na verdade, na configuração B a energia é:
E na configuração A, a energia é:
Logo, a alternativa A está correta!
Na configuração A, o torque é dado por:
Logo, esse não é um valor nulo, e a alternativa B está errada!
Vimos que em um dipolo a força resultante é zero! Portanto tanto em A, quanto em B, a força resultante é zero e essa alternativa está errada!
Na realidade, na configuração B temos um equilíbrio instável (campo e momento de dipolo são anti-paralelos) e não estável (ocorre quando o campo e momento de dipolo são paralelos). E essa alternativa está errada!
A configuração não representa um equilíbrio! Representa um ponto de torque máximo, e o equilíbrio ocorre quando o torque é zero. E essa alternativa está errada!
Resposta
Letra a).