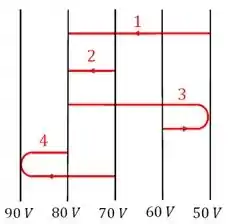
Um elétron vai de uma superfície equipotencial para outra ao longo de um dos quatro
caminhos mostrados na figura abaixo. Classifique os caminhos de acordo com o trabalho realizado pelo campo elétrico ( ), do menor ao maior módulo.
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos lembrar a definição de trabalho.
O trabalho sobre um carga pontual pode ser calculado a partir da seguinte equação
sendo e o potencial sentido pela carga nas posições inicial e final da trajetória, respectivamente.
Note que essa expressão não depende do caminho: só depende dos potenciais nas posições inicial e final da trajetória. Isto porque a força elétrica é uma força conservativa.
Continuando, como estamos interessados no módulo do trabalho, podemos fazer o seguinte.
Antes de prosseguirmos, vamos lembrar de uma unidade de medida de energia muito útil: o elétron-volt. Essa unidade é definida por
A ideia é que é a quantidade de energia cinética ganha por um único elétron quando acelerado por uma diferença de potencial elétrico de , no vácuo.
Na prática, é como multiplicarmos a carga elementar por .Desta forma, o que faremos no próximo passo é calcular o módulo de cada trabalho em elétron-volt para então classificar. SIMBORA!
Passo 2
Pelo caminho 1, vemos que os potenciais nas posições inicial e final são dados por
Assim, o módulo do trabalho no caminho 1 é
Pelo caminho 2, os potenciais nas posições inicial e final são dados por
Assim, o módulo do trabalho no caminho 2 é
Pelo caminho 3, vemos que os potenciais nas posições inicial e final são dados por
Assim, o módulo do trabalho no caminho 3 é
Pelo caminho 4, os potenciais nas posições inicial e final são dados por
Assim, o módulo do trabalho no caminho 4 é
Agora, temos plenas capacidades de classificar os módulos dos trabalhos. Vemos que os mesmos satisfazem
Observando as alternativas, vemos que a alternativa correta é a letra .