Uma carga puntiforme está na origem e uma segunda carga puntiforme está no eixo em . Determine uma expressão para o potencial em qualquer ponto do eixo como uma função de .
Passo 1
Vamos desenhar o que temos nesse problema, uma das cargas está na origem e a outra em e as distâncias são definidas assim
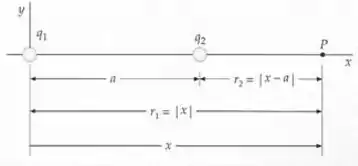
Para resolver esse probleminha, vamos lembrar que o potencial total vai ser a soma dos potenciais devido a cada carga separadamente, ou seja
Passo 2
Substituindo na expressão de o que já temos, vai ficar assim
Repare que quando ou , .
E quando , .
Resposta
Exercícios de Livros Relacionados
Uma placa não condutora infinita possui uma densidade superficial de cargas σ = + 5,80p C / m 2 . (a) Qual é o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q =
Uma esfera não condutora tem raio R = 2,31c m e uma carga uniformemente distribuída q = + 3,50f C . Tome o potencial elétrico no centro da esfera como V 0 = 0 . Determine o valor de V para uma distânc
A abaixo mostra um gráfico da componente x do campo elétrico em função de x em uma certa região do espaço. A escala do eixo vertical é definida por E X S = 20,0 N/C. As componentes y e z do campo elét
Duas placas paralelas condutoras de grande extensão estão separadas por uma distância de 12 cm e possuem densidades superficiais de cargas de mesmo valor absoluto e sinais opostos nas faces internas.
Energia do núcleo. Qual é a energia necessária para montar um nũcleo atômico contendo três prótons (tal como Be), se o modelarmos como um triângulo equilátero de lado 2 ⋅ 10 - 15 m . com próton em cad