Energia Potencial e Densidade de Energia
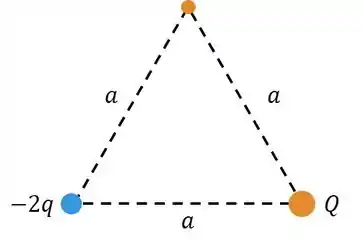
Considere um triângulo equilátero, com aresta de comprimento . Suponha que, em seus vértices, há partículas (pontuais) com cargas , e , conforme mostra a figura abaixo. Qual das opções a seguir fornece corretamente o valor da carga , em função de , para que a energia eletrostática armazenada em tal sistema seja nula?
- Isso é impossível, porque sempre se dispende alguma energia para aproximar corpos carregados.
Passo 1
Recordemos da fórmula da energia potencial para duas cargas:
Para um sistema com mais cargas, a energia total é a soma das energias potenciais duas à duas, ou seja:
Onde os ’s são as distâncias entre os pares de cargas.
Passo 2
Substituindo nesta fórmula os valores dados pelo enunciado:
Ao passo que as distâncias, por se tratar de um triangulo equilátero, são todas iguais à . Logo, podemos colocar em evidência:
Arrumando:
Passo 3
Agora, forçamos a condição pedida pelo enunciado, que é a energia ser igual à zero:
Fim de papo.
Resposta
Letra c.