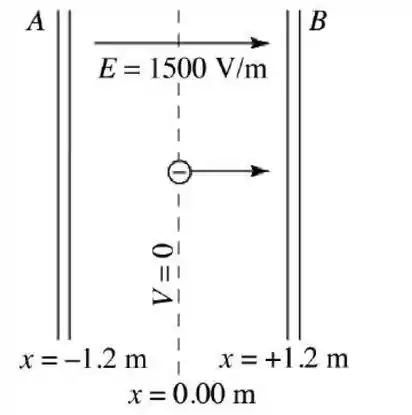
Duas grandes placas paralelas condutoras e estão separadas por . Um campo uniforme de , na direção positiva, é produzido por cargas nas placas. O plano central a é uma superfície equipotencial na qual . Um elétron é projetado a partir de , com uma velocidade inicial de perpendicular às placas na direção positiva, como mostrado na figura abaixo. Qual é a energia cinética do elétron quando atinge a placa A?
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos relembrar o que é o potencial elétrico para um campo elétrico constante.
Considere a figura do enunciado. Sabendo que o campo elétrico é constante entre as placas, dado um ponto de coordenada entre as placas, então o potencial elétrico em é dado por
Assim, se , então . E se , então .
Agora, considere uma carga imerso nesse potencial . A energia potencial elétrica dessa carga é dada por
Assim, dependendo do sinal de e , teremos o sinal de .
Toda essa conversa é pra gente se preparar para aplicar a conservação de energia no nosso problema. Então bora pro próximo passo!!
Passo 2
Já comentamos que vamos aplicar a conservação de energia. Este princípio nos diz que
isto é, a energia mecânica total inicial é igual a energia mecânica total final.
A energia mecânica total é composta pela energia cinética e pela energia potencial do elétron. Assim,
Na situação inicial, temos que o elétron está com velocidade e na posição . Logo,
Na situação final, temos o elétron colidindo com a placa . Assim,
sendo a posição da placa no sistema de coordenadas adotado.
Assim, a equação de conservação de energia retorna
Como a posição final do elétron é a placa , então . Desta forma, utilizando os dados do enunciado e do formulário, temos finalmente que
Observando as alternativas, vemos que a alternativa correta é a letra .