Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Potencial e Trabalho

Ver Teoria
Exercício 61234578910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758

Enunciado

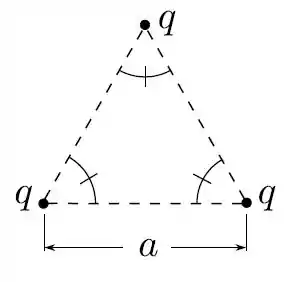
Qual é o trabalho necessário para formarmos a configuração de três partículas, todas com a mesma carga q , supondo que tais partículas estão, de início, infinitamente afastadas?

  1. 2 k 0 q 2 a
  2. 4 k 0 q 2 a
  3. 5 k 0 q 2 a
  4. 6 k 0 q 2 a
  5. 3 k 0 q 2 a

Passo 1

Perguntou o trabalho e tem um triângulo na figura! Essa questão é clássica. Para configurações discretas de cargas nós sabemos a energia potencial que elas armazenam:

U = k q 1 q 2 r 12 + q 2 q 3 r 23 + q 1 q 3 r 13

E também temos a fórmula da relação entre trabalho e variação da energia potencial:

W = - Δ U

Passo 2

Vamos achar a variação da energia. No início ele disse que as cargas estão muito afastadas:

r 12 = r 13 = r 23 → ∞

Que na fórmula vai dar que a energia potencial é zero:

U ≈ 0

E no final nós temos que as distâncias são todas iguais a a e as cargas são iguais a q :

U = k q 2 a + q 2 a + q 2 a

3 k q 2 a

Passo 3

Aplicando a fórmula, temos:

Δ U = U final - U inicial

Δ U = 3 k q 2 a - 0

Δ U = 3 k q 2 a

O trabalho é, portanto:

W = - 3 k q 2 a

Esse seria o trabalho do campo elétrico, certo? Mas pra formar essa configuração, o trabalho é realizado por uma força externa! Como W F ext = - W , onde W é o trabalho do campo que a gente achou:

W F ext = 3 k q 2 a

Logo...

Resposta

Letra e.

Exercícios de Livros Relacionados

Uma placa não condutora infinita possui uma densidade superficial de cargas σ = + 5,80p C / m 2 . (a) Qual é o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q =
Uma esfera não condutora tem raio R = 2,31c m e uma carga uniformemente distribuída q = + 3,50f C . Tome o potencial elétrico no centro da esfera como V 0 = 0 . Determine o valor de V para uma distânc
A abaixo mostra um gráfico da componente x do campo elétrico em função de x em uma certa região do espaço. A escala do eixo vertical é definida por E X S = 20,0 N/C. As componentes y e z do campo elét
Duas placas paralelas condutoras de grande extensão estão separadas por uma distância de 12 cm e possuem densidades superficiais de cargas de mesmo valor absoluto e sinais opostos nas faces internas.
Energia do núcleo. Qual é a energia necessária para montar um nũcleo atômico contendo três prótons (tal como Be), se o modelarmos como um triângulo equilátero de lado 2 ⋅ 10 - 15 m . com próton em cad