UERJ, Sem Campus, Física I, Listas de F1 - Profª Fernanda Deus - Lista 5 - Força e Movimento I, Questão 13b
Três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas são , e . Quando o conjunto é liberado a partir do repouso.
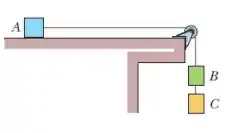
que distância percorre nos primeiros (supondo que não atinja a polia)?
Passo 1
E aí pessoal, tudo tranquilo?
Nessa questão temos um arranjo de fios e caixas, onde a caixa está apoiada sobre uma mesa e as caixas e estão penduradas por um fio. Igual mostrado na figura:
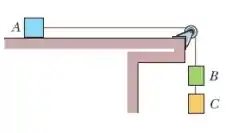
Foram dadas as massas de cada caixa. No item anterior, usamos a segunda lei de Newton para determinar a aceleração do conjunto de caixas, e vimos que:
Nessa item, precisamos determinar a distância que percorre nos primeiros .
Para fazer isso, como trata-se de um movimento com aceleração constante, podemos utilizar a equação horária da posição:
Vamo nessa!
Passo 2
A distância percorrida, , é dada por:
Onde , já que o conjunto parte do repouso, e:
Daí:
Prontinho pessoal!
Curtiram a solução? Responde Aí!