UFCG, Sem Campus, Física I, AV2 - Profº Rômulo Rodrigues - 2022.1, Questão 2
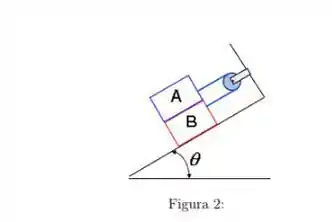
Os dois blocos da Fig.(2) partem do repouso e suas massas são: e . Sabendo que , determine (a) a aceleração de cada bloco e a tensão no cabo. Despreze as massas das polias e os atritos.
Passo 1
Vamos resolver o problema usando as leis da física. Primeiro, lembre-se que a aceleração de ambos os blocos e a tensão no cabo serão as mesmas devido à corda que os conecta. Vamos chamar essa aceleração e tensão de "a" e "T", respectivamente.Dado:
- Massa do bloco A,
- Massa do bloco B,
- Ângulo inclinado,
- Aceleração da gravidade,
Passo 2
Agora, vamos analisar as forças que atuam em cada bloco ao longo do plano inclinado:
Para o bloco A:
- Força de gravidade:
- Componente da força de gravidade ao longo do plano inclinado:
- Força resultante ao longo do plano inclinado:
- Força de gravidade:
- Componente da força de gravidade ao longo do plano inclinado:
- Força resultante ao longo do plano inclinado:
Para o bloco B:
Passo 3
Tensão no cabo: Agora podemos escrever as equações de Newton para cada bloco ao longo do plano inclinado:Para o bloco A:
Para o bloco B:
Passo 4
Substituindo , temos:
Agora podemos resolver esse sistema de equações para encontrar "a" e "T". Somando as duas equações:
Passo 5
Substituindo os valores numéricos, temos:
A aceleração é negativa porque o bloco está descendo o plano inclinado.Agora, podemos usar uma das equações para encontrar a tensão no cabo. Vamos usar a equação para o bloco A:
Substituindo os valores numéricos e resolvendo para "T":
Portanto, a aceleração de cada bloco é aproximadamente , e a tensão no cabo é aproximadamente .
Resposta
Portanto, a aceleração de cada bloco é aproximadamente , e a tensão no cabo é aproximadamente .