Uma cunha, formada pela junção de duas rampas inclinadas de ângulos e , está fixa ao solo. Os blocos de massas e estão ligados por um fio ideal que passa por uma polia ideal fixa no vértice da cunha. Os blocos estão inicialmente em repouso e cada um deles encontra-se em uma das rampas, como mostra a figura.
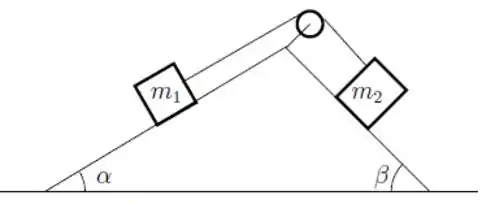
Desprezando o atrito entre os corpos e as superfícies das rampas
a) desenhe o diagrama de forças para cada um dos blocos, separadamente;
b) supondo que as massas sejam tais que o bloco de massa desça a rampa à esquerda, determine o módulo da aceleração ;
c) obtenha a razão para que o sistema permaneça em repouso;
d) de acordo com o item (c), qual o valor da tração no fio?
Passo 1
a)
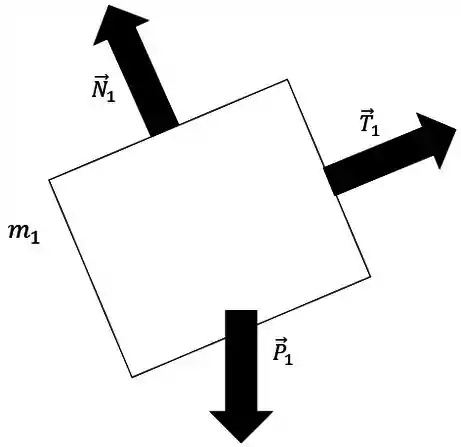
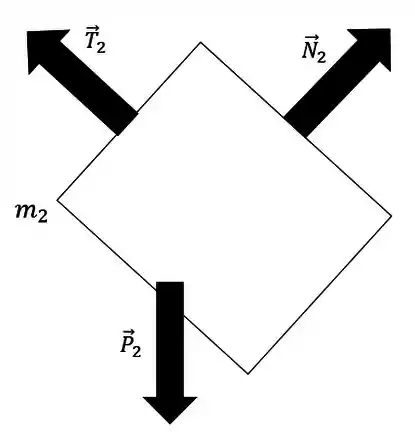
As forças atuando nos blocos são as força peso e , as forças normais da superfície e e as força de tração dos fios e .
O diagrama do bloco de massa é:
E pro bloco de massa :
Passo 2
b)
As forças resultantes atuando nos 2 blocos são:
Então, pela 2ª lei de Newton:
O problema é que, pros 2 blocos, a força peso não faz um ângulo maneiro com normal ou a tração!
Passo 3
Agora fatalmente vamos ter que decompor as forças peso dos 2 blocos, pra elas terem componentes paralelas e perpendiculares às forças normal e de tração. Saca só:
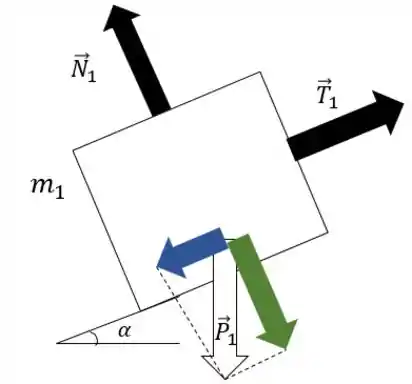
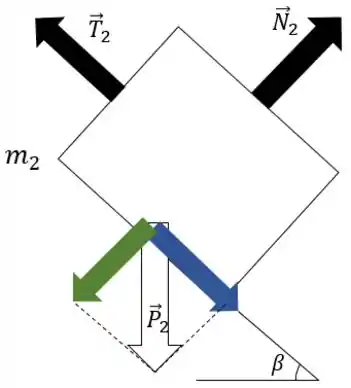
Passo 4
Aplicando uma trigonometria básica, obtemos:
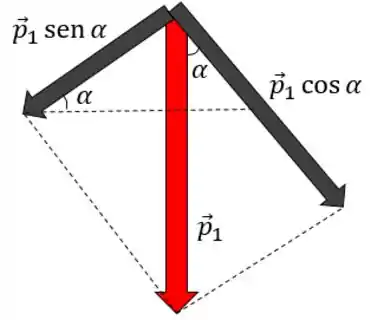
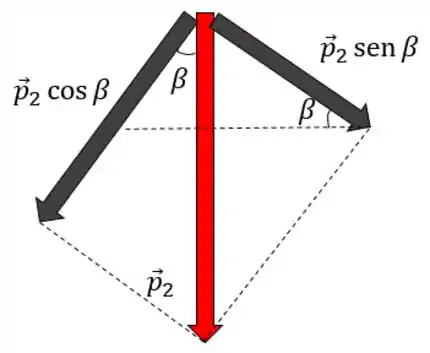
Passo 5
Então o diagrama de forças nos blocos ficou:
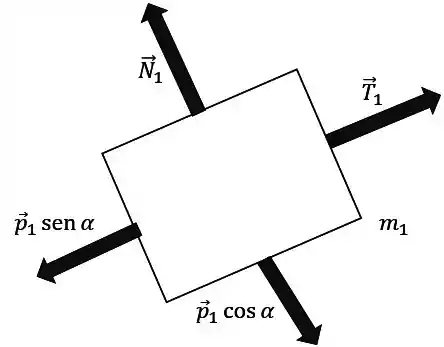
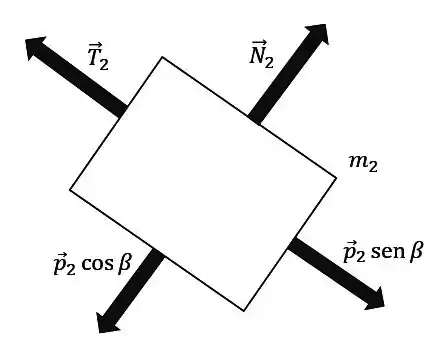
Passo 6
Agora temos que fazer umas considerações importantes. Primeiro, podemos reparar que os fios e as roldanas são ideais, então as trações e tem mesmo módulo, que podemos chamar de :
E não só isso! Pelo mesmo motivo, as acelerações dos blocos também tem o mesmo módulo :
Excelente, né?
Passo 7
Pronto, agora podemos voltar a usar nossa querida 2ª lei de Newton.
Começando pelo bloco de massa :
Não há nenhum movimento no eixo perpendicular à cunha, as forças e se cancelam. O movimento é todo no eixo paralelo à cunha, logo:
Como o bloco está descendo, em módulo isso fica:
Passo 8
Agora vamos ao bloco de massa :
Pra ele também não há movimento no eixo perpendicular à cunha, pois e se cancelam. O movimento é só no eixo paralelo à cunha, então, pela 2ª lei de Newton:
E como o bloco está subindo:
Passo 9
Então obtivemos um sistema:
Vamos somar as 2 equações:
Temos e , logo:
Passo 10
c)
Pra que o sistema fique em repouso, devemos ter
Então a razão entre as massas é
Passo 11
d)
Vimos ali atrás que
Mas agora estamos considerando , logo:
Podemos também expressar em função de e , o que dá
Resposta
a)
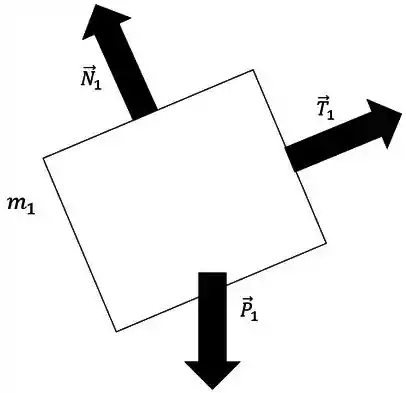
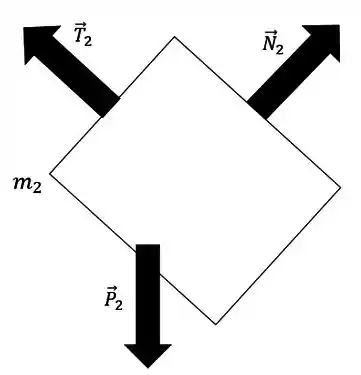
b)
c)
d)
ou