Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Simples

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263

Enunciado

UFCG, Sem Campus, Física I, AV2 - Profº Rômulo Rodrigues - 2022.1, Questão 1

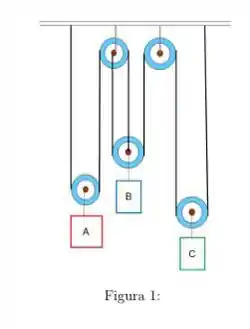
Determine as acelerações de cada bloco da Fig.(1), considerando que as massas dos blocos A, B e C são respectivamente: 10 K g , 20 K g e 10 K g .

Passo 1

E aí gurizada, vamos para mais uma questão de física!!

Temos um sistema com 5 polias, sendo 3 móveis e 2 fixas, e três blocos A , B e C pendurados. Para calcular as acelerações de cada bloco, precisamos considerar as forças envolvidas, como tensões nas cordas e forças de gravidade.

Passo 2

O próximo passo seria considerar as forças envolvidas, aplicar a Segunda Lei de Newton 98 ( F = m * a para cada bloco, considerando as tensões nas cordas, a força de gravidade e as acelerações das polias.Primeiro, vamos calcular as forças de gravidade em cada bloco:

B l o c o   A :   M a s s a   =   10   k g ,   F o r ç a   d e   G r a v i d a d e   ( P e s o )   =   m x   g =   10   k g   x   9,8   m / s ²   =   98   N

  B l o c o   B :   M a s s a   =   20   k g ,   F o r ç a   d e   G r a v i d a d e   ( P e s o )   =   m x   g =   20   k g   x   9,8   m / s ²   =   196   N

  B l o c o   C :   M a s s a   =   10   k g ,   F o r ç a   d e   G r a v i d a d e   ( P e s o )   =   m   x   g =   10   k g   x   9,8   m / s ²   =   98   N

Passo 3

Agora, vamos considerar as tensões nas cordas. Nas pólias fixas, a tensão não muda de direção. Nas pólias móveis, a tensão muda de direção, mas sua magnitude é a mesma em ambos os lados da pólia. Vamos chamar as tensões de T1, T2 e T3, como mostrado na Figura

Agora, aplique a segunda lei de Newton (F = ma) a cada bloco:

Para o Bloco A:

T 1   -   98   N   =   10   k g   *   a   ( E q u a ç ã o   1 )

Para o Bloco B:

T 2   -   196   N   =   20   k g   *   a   ( E q u a ç ã o   2 )

Para o Bloco C:

T 3   -   98   N   =   10   k g   *   a   ( E q u a ç ã o   3 )

Agora, você tem um sistema de três equações (Equações 1, 2 e 3) com três incógnitas (T1, T2 e T3). Resolva esse sistema de equações para encontrar as tensões nas cordas e, consequentemente, a aceleração (a) que é comum a todos os blocos. Isso permitirá determinar as acelerações de cada bloco no sistema de polias.

Passo 4

F o r ç a s   d e   G r a v i d a d e :

B l o c o   A : F = m * a = 10   k g ⋅ 9.8   m / s 2 = 98   N F   g A ​   = m   A ​   ⋅ g = 10 k g ⋅ 9.8 m / s ²   98 N

B l o c o   B :   F = m * a = 20   k g ⋅ 9.8   m / s 2 = 196   N F   g B ​   = m   B ​   ⋅ g = 20 k g ⋅ 9.8 m / s   2   = 196 N

B l o c o   C :   F = m * a = 10   k g ⋅ 9.8   m / s 2 = 98   N F   g C ​   = m   C ​   ⋅ g = 10 k g ⋅ 9.8 m / s   2   = 98 N

  • Relação entre Tensões nas Cordas:

Como temos cinco polias (três móveis e duas fixas), a tensão em cada lado da polia móvel é igual.,

Agora, vamos considerar o sistema de polias e as acelerações:

  • Para o Bloco A:
    • A única força horizontal é na direção positiva.

Como todas as massas estão interligadas pelo mesmo sistema de cordas e polias, elas têm a mesma aceleração

T 1 ​ − F g A ​ = m A ​ ⋅ a T 1 ​ − F g B ​ = m B ​ ⋅ a   T 1 ​ − F g C ​ = m C ​ ⋅ a

Resposta

T 1 ​ − F g A ​ = m A ​ ⋅ a T 1 ​ − F g B ​ = m B ​ ⋅ a   T 1 ​ − F g C ​ = m C ​ ⋅ a

Exercícios de Livros Relacionados

Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con
Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m
Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in
Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo
Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es