UERJ, Sem Campus, Física I, Listas de F1 - Profª Fernanda Deus - Lista 5 - Força e Movimento I, Questão 14b
A figura mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa , o outro tem massa .
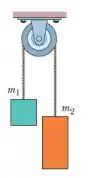
Qual é a tensão da corda?
Passo 1
E aí galerinha do bem, tudo tranquilo por aí?
Nessa questão temos um conjuntinho de dois blocos ligados por um fio, que passa por uma polia fixa no teto. As massas dos blocos são dadas. Precisamos determinar a tensão na corda.
Para fazer isso, vamos desenhar o diagrama de forças nos blocos para escrever a equação da segunda lei de Newton em cada um deles. É importante ficarmos ligados que, como o comprimento do fio é constante, os blocos precisam ter a mesma aceleração, beleza?
Vamo nessa!
Passo 2
Bom, em cada um dos blocos atua a força peso e a força de tração.
Como vamos supor que ele irá descer, enquanto irá subir.
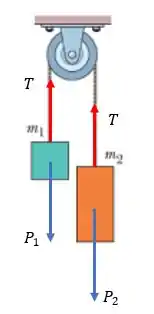
Daí, escrevendo a equação da força resultante para cada um dos blocos, e considerando que o bloco irá descer, temos:
Pra calcularmos a aceleração dos blocos basta somarmos as duas equações:
Substituindo os valores das massas dados no enunciado, vem que:
Logo:
Passo 3
Agora que conhecemos a aceleração é só voltarmos pra equação da força resultante:
Logo:
Uhuuuul! Terminamos!
Valeu gente!!