Três massas, , e estão penduradas nas cordas de polias como mostra a figura, A massa é maior que a soma das outras duas outras massas. As cordas e as polias têm massa desprezível.
a) Isole os corpos e desenhe o diagrama de forças atuando em cada massa.
b) A partir da lei de Newton escreva as equações de movimento para cada massa.
c) Encontre a aceleracao da massa .
d) Encontre as tensões nas cordas ligadas às massas e .

Passo 1
Fazendo o diagrama de cada um dos bloquinhos:
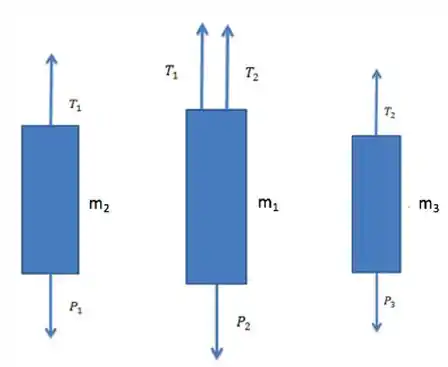
Passo 2
O enunciado nos diz que a massa central é a maior. Logo, podemos supor que ela está descendo e as outras subindo, fechou?
Assim, teremos as seguintes equações:
Passo 3
Letra c)
Pra achar a aceleração vamos fazer um joguinho algébrico.
Sabe aquelas três equações que achamos na letra anterior? Então, é só somar elas três e isolar a aceleração!
Juntando as paradas que tão em comum em cada lado e isolando a aceleração vai ficar assim ó:
Isolando o :
Passo 4
Letra d)
Pra achar as tensões fica fácil agora que já descobrimos a aceleração. Primeiro temos que isolar a tensão em cada uma das duas últimas equações
Agora é só substituir a aceleração .Depois disso é só álgebra! Organizando tudo que tem ali vamos ficar com a resposta final:
Resposta
- ; ;
- ;