O plano abaixo tem inclinação em relação à horizontal igual a . Duas cordas inextensíveis e uma polia, ambas sem massa, mantém em equilíbrio três caixas. Despreze o atrito entre as caixas e o plano. Responda aos itens abaixo, sabendo que a caixa tem massa igual a , a caixa tem massa igual a , e que .
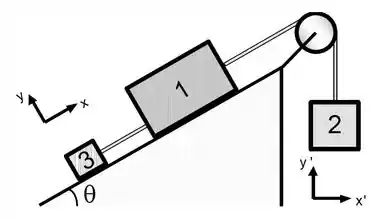
Escreva a expressão literal para as equações de movimento das três caixas, em termos das suas componentes, utilizando os respectivos sistemas de coordenadas indicados na figura. Em seguida calcule o valor da massa da caixa .
Calcule e escreva utilizando notação vetorial a força normal que a caixa exerce sobre o plano.
Suponha agora que a caixa tem massa igual a . Calcule a componente horizontal da aceleração da caixa .
Passo 1
Antes de escrever as equações, vamos primeiro fazer o diagrama do corpo livre, o famoso DCL.
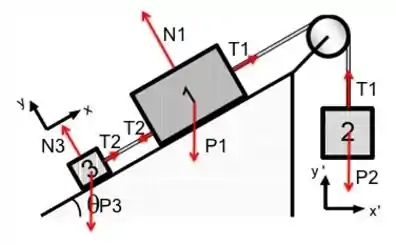
Agora que sabemos quais forças e como elas atuam nos corpos, podemos montar as equações do movimento.
Passo 2
De acordo com a segunda Lei de Newton, teremos que o somatório de forças em cada corpo é igual ao produto de sua massa vezes a aceleração. Como todos os corpos estão ligados por fios inextensíveis, teremos que essa aceleração será a mesma para todos os corpos, e iremos adotar para designá-la. Vamos decompor o movimento nas duas componentes para ficar mais fácil a visualização. Lembrando que iremos utilizar o sistema de coordenas para os corpos e e o sistema para o corpo !
Agora, podemos começar, para o corpo , temos:
Em :
Em , como não há movimento, temos:
Para o corpo , temos:
Em :
Em , como não há movimento, temos:
Para o corpo , como temos somente movimento em ’, temos:
Em ’:
Passo 3
Para determinar a massa do corpo , vamos somar todas as equações de movimento em e em , de modo a cancelar os valores que não temos:
Somando, temos:
Como temos que o sistema está em equilíbrio, sabemos que
Para achar a massa do corpo , basta substituir os valores:
Passo 4
Pela equação do movimento em para o corpo , temos:
Teremos, em módulo:
Como ele pede a força normal que o bloco faz no plano, teremos, vetorialmente, que:
Veja que essa não é a força normal que desenhamos no diagrama do corpo livre. A desenhada é a força que o plano faz no bloco. Ela será igual em módulo e sentido, mas a direção será contrária.
Passo 5
Agora as coisas ficam um pouco diferentes, o sistema sairá da situação de equilíbrio. As equações de movimento que montamos no item ainda estão valendo, só que agora, será diferente de zero. Retomando a equação que já tínhamos achado, temos:
Para determinar a aceleração, é só substituir os valores conhecidos:
Achamos um valor negativo, pois essa aceleração aponta para baixo, no caso do bloco .
Para determinar a componente horizontal da aceleração da caixa , basta decompor, teremos:
Resposta