Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Simples

Ver Teoria
Exercício 501234567891011121314151617181920212223242526272829303132333435363738394041424344454647484951525354555657585960616263

Enunciado

USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 36

36. Um bloco de massa m 1 , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M , a uma massa suspensa m 2 m 2 > m 1 . O sistema é solto em repouso. Calcule, por conservação da energia, a velocidade v de m 2 após cair de uma altura h .

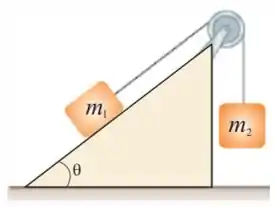
Passo 1

Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nosso objetivo nesse problema é calcular a velocidade v do bloco m 2 após cair uma altura h no sistema descrito no enunciado.

Pra isso foi pedido pra usarmos a lei de conservação de energia.

Parece tranquilo? 😬

Pela lei da conservação de energia temos que a energia mecânica inicial é igual a energia mecânica final ou também podemos dizer que a variação da energia potencial do sistema é igual a variação da energia cinética, ou seja

∆ E c = W

O trabalho realizado pelos blocos pode ser calculado como a força gravitacional multiplicada pelo deslocamento em y .

Já a variação da energia cinética é atribuída ao movimento dos blocos e a rotação da polia...

Sacou como podemos resolver esse problema? 😎

Passo 2

Vamos começar escrevendo a equação da energia cinética do sistema, que será nada mais que a soma das energias de cada componente...

Para o bloco 1 , temos

E 1 = m 1 v 2 2

Para o bloco 2

E 2 = m 2 v 2 2

E para a polia...

E p = I ω 2 2

Substituindo na variação da energia cinética...

∆ E c = m 1 v 2 2 + m 2 v 2 2 + I ω 2 2

O momento de inercia de uma polia é o mesmo de um disco, ou seja

I = M R 2 2

Podemos relacionar a velocidade angular ω com a velocidade v sabendo que

ω = v R

Substituindo na equação...

∆ E c = m 1 v 2 2 + m 2 v 2 2 + M R 2 2 v R 2 2

∆ E c = m 1 v 2 2 + m 2 v 2 2 + M R 2 v 2 4 R 2

∆ E c = v 2 m 1 2 + m 2 2 + M 4

Tranquilo até aqui? 😉

Passo 3

Agora calculando o trabalho realizado pelo deslocamento dos blocos, temos

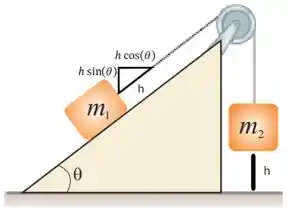
Pela figura, podemos ver que o bloco 1 se move h sin ⁡ θ na vertical e o bloco 2 se move h .

Como o trabalho é igual a força multiplicada pelo deslocamento, então

W = m 2 g h - m 1 g h sin ⁡ θ

O trabalho do bloco 1 é negativo pois o deslocamento é contrário à força.

Igualando ∆ E c com W

∆ E c = W

v 2 m 1 2 + m 2 2 + M 4 = m 2 g h - m 1 g h sin ⁡ θ

Isolando v e simplificando...

v 2 = m 2 g h - m 1 g h sin ⁡ θ 1 2 m 1 + m 2 + M 2

v 2 = 2 m 2 g h - m 1 g h sin ⁡ θ m 1 + m 2 + M 2

v = 2 m 2 g h - m 1 g h sin ⁡ θ m 1 + m 2 + M 2

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

v = 2 m 2 g h - m 1 g h sin ⁡ θ m 1 + m 2 + M 2

Exercícios de Livros Relacionados

Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con
Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m
Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in
Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo
Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es