Em um máquina de Atwood dois blocos de massa e estão ligados por uma corda de massa desprezível que passa por uma polia de raio R = 10 cm e massa .
a) Se não há deslizamento entre a corda e a polia, calcule a tração em cada trecho da corda que liga os blocos e a força no suporte que liga a polia ao teto.
b) Se abandonados do repouso, calcule a velocidade dos blocos depois que o bloco mais pesado desce uma distância de .

Passo 1
O legal de problemas com polias, é que eles são fáceis de se analisar. Podemos mostrar isso aqui e você sairá desse exercício sem mais dúvidas.
A primeira coisa que podemos fazer antes de realmente colocar a mão na massa é descrever o diagrama de forças, assim ficará bem mais fácil de saber para onde devemos ir.
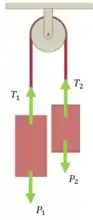
Uma coisa que é importante a gente conversar agora antes que chegue matérias mais avançadas, são os vínculos. Os vínculos como o nome sugere seriam variáveis ou equações que ligam, em casos mais simples, os corpos.
Em nosso caso perceba que claramente o que liga os dois blocos é uma corda. Assim o movimento de um bloco afeta diretamente o outro bloco. Mas e agora algebricamente, quem é o vínculo? Se você disse a posição, velocidade ou aceleração vocês acertaram e são com isso que iremos trabalhar...
Passo 2
(a) Mesmo que a gente não olhasse pro diagrama acima, você concorda que todo mundo que olhar para esse problema sabe o que vai acontecer? A massa do bloco da esquerda é mais pesada que o bloco da direita. Desta forma o bloco da esquerda irá cair e da direita irá subir. Assim tome que
Perceba que a ordem na qual foram escritos nossos e importa.
Por fim temos que o giro da polia gera um torque, giro esse que ocorre porque uma força atua na polia, ou seja
Como estamos lidando com um disco, tome que o momento de inércia de um disco é . Assim
Observe que a aceleração angular que do disco está ligada a aceleração da corda, mas a corda não era um vínculo dos blocos? Pois bem estão temos que todos os corpos do nosso problema estão ligados. Mas como ligamos a polia de maneira algébrica? Pois bem
Então temos finalmente um sistema com 3 equações
Passo 3
Vamos resolver esse nosso problema de maneira simples agora. Vamos somar tudo ...
Ficando assim com
Que resolvendo
E agora podemos finalmente determinar nossas trações.
Enquanto
Finalmente temos que a força que segura tudo isso ao teto é descrito por
Passo 4
(b) Podemos começar e terminar nosso problema chamando nosso grande amigo Torricelli, na qual
Sabemos que a massa é abandonada do repouso, então . Também sabemos que a aceleração é e que , então teremos que
então
Resposta
- , e