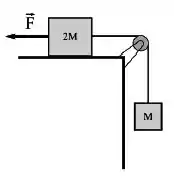
Se e , qual é a tensão na corda que conecta dos dois blocos da figura abaixo? Suponha que não há atrito entre as superfícies e que a massa da corda seja desprezível.

Dado:

(a)

(b)

(c)

(d)

(e)

Vamos analisar cada um desses blocos pelo diagrama de corpo livre (DCL).

Para o bloco de massa :

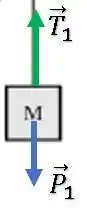
Considerando que o bloco está subindo (hipótese a ser confirmada), podemos aplicar a segunda lei de Newton:

Já para o bloco de massa :

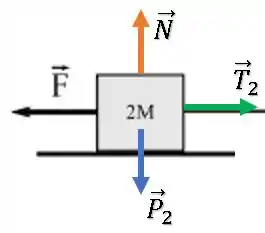
Temos um equilíbrio de forças na vertical, então, já que o bloco se move para direita (hipótese a ser confirmada) a segunda lei de Newton fica:

Agora, podemos juntar as duas equações encontradas.

Já que a corda e a polia (não diz nada sobre) são ideais, podemos dizer que a tração ao longo de todo o cabo é a mesma:

Além disso, ainda porque a corda é ideal, as acelerações dos dois blocos devem ter o mesmo módulo, então:

Assim, podemos chamar as acelerações de e as forças de tração de :

Para achar o valor de , um dos caminhos é dividir uma equação pela outra.

A força peso no bloco de massa é:

Logo:

Substituindo os valores:

Como achamos um valor positivo para a força de tração, significa que a hipótese que fizemos sobre o sentido do movimento está correta.

Assim, ficamos com a alternativa (b).