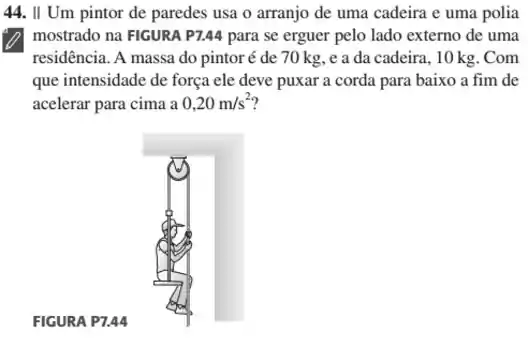
Passo 1
Podemos representar a figura do problema da seguinte forma:
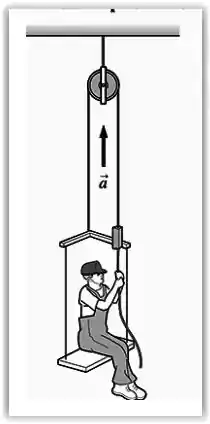
Vamos primeiro entender o diagrama de forças que atua no problema:
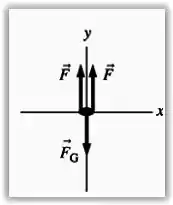
Temos as duas forças , que a corda faz no pintor e o peso do sistema pintor + cadeira ().
Se repararmos, a força que o pintor fará para baixo é justamente a tensão na corda.
Assim, podemos usar a Segunda Lei de Newton para o diagrama que montamos:
Substituindo os valores:
Resposta
a)
Exercícios de Livros Relacionados
Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con
Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m
Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in
Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo
Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es