Exercícios Resolvidos de Polias Simples

Exercício 43 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

Enunciado

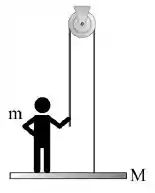
Um homem está sobre uma plataforma. O homem mantém a plataforma em repouso através de uma corda que passa por uma polia presa ao teto, como na figura. As massas da corda e da polia podem ser desprezadas, assim como o atrito na polia. Se o homem tem massa e a plataforma tem massa , qual é o módulo da força que o homem precisa fazer para manter a plataforma em repouso? (Dica: Faça diagramas de corpo livre antes de responder!)

(A)

(B)

(C)

(D)

(E)

Passo 1

Vamos analisar as forças sobre o homem e a plataforma separadamente.

No homem, temos uma força peso, uma força normal de contato com a plataforma e a força e tração na corda:

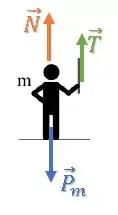
Passo 2

Já a plataforma, temos sua força peso, uma força normal que o homem exerce sobre ela e ainda a força de tração da corda:

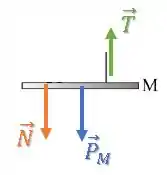
Passo 3

Ficamos com um sistema assim:

Somando as duas equações, chegamos em:

Ficamos com a alternativa (E).

Resposta

Letra (E)

Exercícios de Livros Relacionados

Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con

Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m

Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in

Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo

Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es