USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 27b
Dois blocos estão ligados por um fio de massa desprezível passando sobre uma polia de raio e momento de inércia . O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração constante de .
Encontre o momento de inércia da polia.
Passo 1
Eaew, tudo bem?
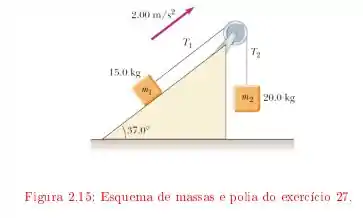
Temos o seguinte esquema para este problema
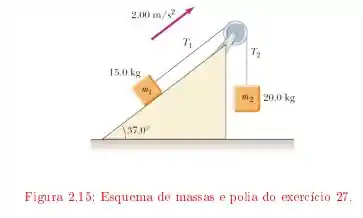
Note que temos dois blocos com massas e ligadas por uma corda inextensível, no sistema temos uma polia cujo raio é e momento de inércia . Usando o dado que a aceleração do sistema é , precisamos
Encontre o momento de inércia da polia.
na questão anterior encontramos que
e
esse resultado será importante pois podemos obter o momentum de inércia desejado pela segunda lei de Newton das rotações
em que o torque resultante é devido às tensões na corda atuando sobre a polia! A aceleração angular será relacionada a aceleração do sistema através de
em que é o raio da polia! Vamos fazer as contas agora!
Passo 2
O torque resultante será obtido como
Temos que é a favor da rotação da polia e é contrário, portanto, temos que a força resultante será tal que
a aceleração angular é tal que
de forma que o momentum de inércia será
A questão foi isso! Te vejo na próxima! Tchau Tchau!