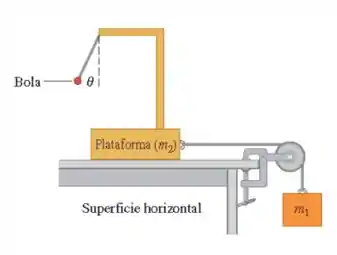
O sistema representado na figura abaixo pode ser usado para medir a aceleração do sistema. Um observador se movendo na plataforma mede o ângulo que o fio que suporta a bola de luz faz com a vertical. Não existe atrito em nenhum lugar. (a) Como está relacionado com a aceleração do sistema? (b) Se e o que é ? (c) Se você pudesse alterar qual é o maior ângulo que você poderia obter? Explique como você deve ajustar para fazer isso.
Passo 1
Alôôô, é aqui que temos alunos aplicadíssimos e animados com essa questão??

Ebaa, é sim!! Vamos então…
Bom então temos nessa questão todo um sisteminha com dois pesos, uma polia, um fio e uma bolinha de luz. Todo esse experimento serve para medir a aceleração do sistema, uma vez que como todo o sistema está interligado todos os 3 objetos terão a mesma aceleração em módulo.
Sendo assim, temos a missão de primeiro encontrar a relação entre o ângulo do fio e a aceleração, em seguida temos que calcular esse ângulo de acordo com os valores de massa fornecidos e por fim, temos que relacionar o valor das massas com o ângulo em questão de modo que se obtenha o seu valor máximo.
Passo 2
Vamos começar analisando as forças na bola:
Isso porque na vertical as forças que atuam sobre a bolinha se equilibram. Adotando -se o sentido positivo para cima temos,
Cuidado para não se confundir, aqui a componente vertical será a intensidade da força vezes o cosseno ( e não o seno como de costume)!
Já analisando as forças em relação ao eixo x:
Uma vez que o sistema possui aceleração, logo há uma força resultante atuando sobre a bolinha fazendo com que essa tenha uma angulação em relação a vertical.
Dividindo por :
Então, conseguimos obter uma relação entre o ângulo e a aceleração!!!
Passo 3
Analisando as forças para a plataforma:
Como a plataforma está apoiada em uma superfície não se tem forças na vertical que a fariam sair voando por exemplo hahaha sendo assim é importante dar atenção apenas para as forças na horizontal
Logo,
Agora analisando as forças no bloquinho suspenso:
Uma vez que o bloquinho pode se movimentar verticalmente!
Como a tendência do bloquinho é descer por isso que subtraio a tensão da força peso e não o contrário.
Substituindo :
Além disso, descobrimos no passo anterior que , substituindo esse resultado na equação encontramos que
No item b, devemos encontrar o ângulo para as massas de e . Como já descobrimos a equação que relaciona as massas com o ângulo basta substituirmos esses valores na equação :
E agora??? Como vamos achar o ângulo a partir da tangente???

Calma que eu te ajudo! Basta utilizarmos a função inversa da tangente que é o arco-tangente, utilizando essa função obtemos nosso ângulo bonitinho,
Passo 4
Agora tá faltando só a cereja do bolo para finalizarmos essa questão. Hummm

Qual o maior ângulo que poderíamos obter nessa questão??? Bom, encontramos o ângulo em função da tangente então o maior ângulo que poderíamos obter é quando a tangente é máxima, ou seja, . Com essa constatação podemos inferir o que sobre as massas?
Caso a tangente seja máxima:
Logo,
Para isso ser verdade a massa de teria que ser muitooooo maior que :
Portanto, a condição para se obter um ângulo de inclinação máximo teríamos que ter um bloquinho muito mais pesado que a plataforma.
Além disso, o fato do ângulo ser máximo indica que
Assim, teríamos que a tração seria zero e conclui-se que a bolinha estaria em repouso em relação a plataforma por não haver mais uma aceleração diferente da gravidade.
Tudo tranquilo??? Deu medo no começo mas foi só sucesso depois hahaha :)
Bora terminar essa lista!
Resposta
- para se obter o ângulo máximo de , e além disso a bolinha estaria em repouso em relação a plataforma.