UERJ, Sem Campus, Física I, Listas de F1 - Profª Fernanda Deus - Lista 5 - Força e Movimento I, Questão 6
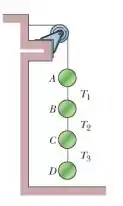
A figura mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas do disco e ?
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão temos um arranjo de discos pendurados através de fios, sendo presos um no outro, conforme mostra a figura abaixo:
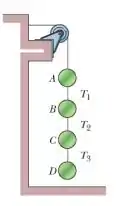
São dadas as tensões em cada um dos fios:
Além da tensão no fio preso na parede e no disco , que vale:
A partir dessas informações precisamos determinar as massas de cada um dos discos.
Basicamente, precisamos verificar o equilíbrio de forças agindo em cada um dos discos. Então, vamos começar fazendo um diagrama de forças geral pros discos, e depois usamos o equilíbrio pra igualar forças!
Vamo nessa!
Passo 2
Em cada um dos discos agem duas forças de tração (do fio acima e abaixo do fio), bem como a força peso. Então, podemos montar um diagrama geral de forças neles da seguinte forma:
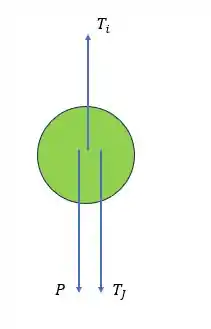
e vai depender do disco que estamos analisando. Mas, de forma geral, podemos escrever a força resultante nos discos como:
Como os discos estão suspensos, ou seja, em equilíbrio, temos:
Daí, isolando o peso:
Logo:
Tranquilo? Então, vamos analisar cada um dos discos individualmente.
Passo 3
Para o disco , acima dele está o fio que vai preso na parede e vale:
Abaixo dele temos o fio , que vale:
Logo, a massa de vale:
Já para , temos o fio acima , e o abaixo :
Para o disco , temos o fio acima e o abaixo :
Por fim, para o disco , temos apenas o fio acima e o peso do disco para baixo.
Assim:
Prontinho pessoal! Curtiram a solução?
Responde Aí!