Dois blocos de massa estão unidos por um fio de massa desprezível que passa por uma roldana com um eixo fixo. Inicialmente o sistema estava em repouso. Um terceiro bloco de massa é então colocado suavemente sobre um dos blocos, como mostra a figura a seguir.
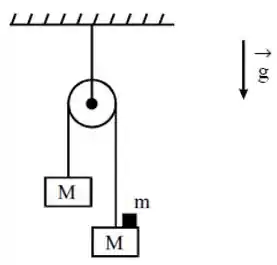
a) Faça um desenho esquemático mostrando as forças que atuam em cada um dos três blocos.
b) Qual é o módulo da aceleração adquirida pelo sistema após o bloco de massa ser colocado?
c) Supondo que o bloco da esquerda estava a uma altura abaixo do bloco da direita quando o terceiro bloco foi posicionado, determine o instante de tempo no qual os dois blocos se cruzarão.
d) Qual é o módulo da força com a qual esse pequeno bloco de massa pressionará o bloco sobre o qual foi colocado?
Passo 1
(a)
Vamos desenhar as forças que estão atuando. Já coloquei um eixo de referencia também.
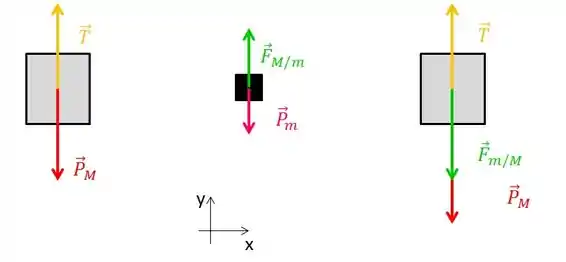
Passo 2
(b)
Vamos aplicar a segunda lei de Newton para cada um dos corpos, lembrando que o movimento do bloco da esquerda é pra cima, e dos da direita é pra baixo. Além disso,
Para o bloco da esquerda:
Para o bloco pequeno:
Para o bloco da direita:
Da primeira equação tiramos que:
Somando a segunda e terceira, temos:
Substituindo T:
Resolvendo isso:
Show!!
Passo 3
(c)
No inicio eles estão separados de uma distância h. conforme o bloco da direita começa a descer, o da esquerda sobe. Então eles vão se encontrar no meio do caminho, ou seja, quando o da direita descer .
Usando a equação da posição em função do tempo, considerando e :
Substituindo os valores:
Então:
Passo 4
(d)
Vimos que
Pela equação que veio da segunda lei d enewton, lá no passo 2:
Substituindo o valor da aceleração:
Arrumando isso:
Uhuul!! Arrasamos!
Resposta
a)
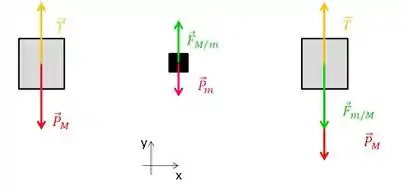
b)
c)
d)