Inicialmente o sistema de corpos mostrado na figura parte do repouso. Todas as superfícies, polia e rodas são sem atrito. O corpo de massa é preso ao corpo de massa , podendo deslizar verticalmente sem atrito, mas não podendo se afastar dele.
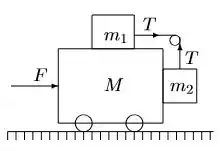
a) Qual é a força horizontal que tem de ser aplicada ao carro para que os blocos permaneçam estacionários em relação ao carro?
Para , no instante após ser solto o sistema de corpos, encontre:
b) A tensão no fio.
c) A aceleração de .
d) A aceleração de .
e) A aceleração de .
Passo 1
a)
Para que não se movimente em relação a , ele tem que ter a mesma aceleração que todo o conjunto.
A aceleração do conjunto vai ser
Já no bloco de massa a força resultante é a tração, assim
Como queremos que o bloco não se mova em relação ao bloco grande temos que o bloco também não pode se mover. Assim, escrevendo a segunda lei na vertical pro segundo bloco
Se jogarmos esse valor de na aceleração do bloco ficamos com
Agora só falta impor que
Isolando
Passo 2
b)
Nesse caso, os três blocos vão ter acelerações diferentes. O bloco estará sujeito a uma aceleração para a esquerda devido à força de reação a tração no bloco . O bloco estará sujeito a uma aceleração para baixo devido à gravidade. O bloco estará sujeito às duas acelerações, e portanto, sua aceleração será a diferença entre elas, .
Agora que já está tudo explicado, vamos aos cálculos. Vamos aplicar a segunda lei de Newton:
Para o bloco :
Para o bloco :
Dividindo tudo por :
Para o bloco :
Agora é só substituir as e na primeira equação:
Passo 3
c)
Da equação temos:
Substituindo o valor da tração:
Passo 4
d)
Da equação temos:
Substituindo o valor da tração:
Passo 5
e)
Da equação temos:
No bloco , temos que a aceleração é dada por:
Resposta
a)
b)
c)
d)
e)