Duas massas e são ligadas por um fio sem massa. A massa desliza por uma superfície horizontal sem atrito e desce por uma polia sem massa e sem atrito. Qual será a massa pendente se a massa e a tração no fio forem conhecidas?
A.
B.
C.
D.
E.
Passo 1
A situação do problema é essa aqui:
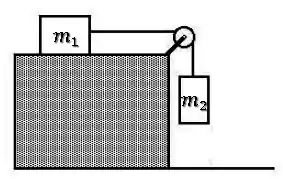
Nosso objetivo é achar sendo conhecidos os valores de e da tração .
Para isso, vamos analisar as forças sobre cada um dos blocos e depois aplicar a segunda lei de Newton.
Passo 2
As forças sobre o bloco 1 são:
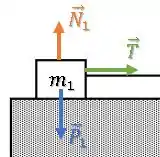
Como não há nenhuma aceleração na vertical, a segunda lei de Newton nessa direção fica:
Mas, nessa questão conseguiremos resolver apenas utilizando a Segunda lei de Newton na direção horizontal:
Passo 3
As forças sobre o bloco 2 são:
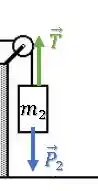
O bloco de massa está descendo e sua aceleração é para baixo, então a segunda lei fica:
Passo 4
Beleza, conseguimos três equações, mas aquela primeira não vai ser útil para relacionar os termos , e , pois ela acrescenta um novo valor desconhecido ().
Então, ficamos com as equações:
Nosso objetivo é achar uma expressão para .
Temos todos os outros parâmetros como dados, exceto a aceleração .
Então, uma boa estratégia é substituir o da primeira equação na segunda para fazer com que ele suma:
Substituindo isso na segunda equação, temos:
Ficamos com a letra (D).
Resposta
Letra (D)