Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO de 2ª Ordem com Coeficientes Constantes – Função Degrau e Delta de Dirac

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657

Enunciado

UNICAMP – Cálculo 3 – 2020.2 – Exame – Exercício 3

Considere o PVI dado por

x ' ' t - x t = a   δ t - 1 ,                   x 0 = 0 ,             x ' 0 = 1 ,

onde a é uma constante real.

a) Resolva tal problema usando transformadas de Laplace. Simplifique sua solução ao máximo em cada uma das regiões dadas por 0 < t < 1 e t > 1 .

b) Tome agora a = - e , onde e é a constante de Euler. Resolva tal PVI no Mathematica (ou Wolfram) pelo método que você preferir e faça o gráfico de sua solução. Qual é o máximo valor (aproximadamente) assumido por sua solução?

Passo 1

Fala galerinha, beleza? Bora resolver uma questão de EDO!

O problema quer que a gente resolva a EDO usando transformadas de Laplace. Só para recordar, a transformada de Laplace F s de uma função f t é

F s = L f = ∫ 0 ∞ f t   e - s t   d t

A EDO pode ser escrita como

d 2 x d t 2 - x = a   δ t - 1

Vale lembrar que δ é a função delta de Dirac. Se você não faz ideia do que são essas coisas, aconselho você dar uma olhadinha nos resumos do RespondeAí sobre transformada de Laplace e depois voltar aqui!

Passo 2

O método para resolver a EDO é tomar a transformada de Laplace dos dois lados:

L x ' ' t - x t = L a   δ t - 1

Usando as propriedades de linearidade:

L x ' ' t - L x t = a   L δ t - 1

A transformada de Laplace para a segunda derivada é

L x ' ' t = s 2 L x t - s   x 0 - x ' 0

Usando as condições iniciais x 0 = 0 e x ' 0 = 1 , temos que

L x ' ' t = s 2 L x t - 1

Vale destacar que essa fórmula da transformada de Laplace da segunda derivada foi dada no formulário da prova e nos resumos do RespondeAí discutimos isso em detalhe!

Substituindo a transformada de x ' ' na equação:

s 2 L x t - 1 - L x t = a   L δ t - 1

s 2 - 1   L x t - 1 = a   L δ t - 1

Nos resta calcular a transformada de Laplace da função delta de Dirac:

L δ t - 1 = ∫ 0 ∞ δ t - 1   e - s t   d t

É importante você lembrar a seguinte propriedade da função delta:

∫ δ t - a   f t   d t = f a

Com isso,

L δ t - 1 = e - s ⋅ 1 = e - s

Portanto, nossa equação fica

s 2 - 1   L x t - 1 = a e - s

Isolando L x t :

L x t = 1 + a e - s s 2 - 1

Para achar a solução da EDO, temos que computar a transformada inversa de Laplace para encontrar x t .

Passo 3

Para fazer a transformada inversa, vamos quebrar a expressão em duas:

L x t = 1 s 2 - 1 + a e - s s 2 - 1

Vamos escrever ainda

1 s 2 - 1 = A s - 1 + B s + 1 = A s + A + B s - B s 2 - 1

Logo,

A + B = 0 A - B = 1 → A = 1 2           e             B = - 1 2

Portanto,

L x t = 1 2 ⋅ 1 s - 1 - 1 2 1 s + 1 + a 2 ⋅ e - s s - 1 - a 2 ⋅ e - s s + 1

Agora olha que legal: a gente sabe que:

L e k t = 1 s - k

Logo, fazendo a inversa:

L - 1 1 s - k = e k t

Portanto,

L - 1 1 s - 1 = e t                 e             L 1 s + 1 = e - t

Para fazer a transformada inversa dos outros termos, vamos considerar a relação

L - 1 e - c s   L f t = f t - c   u t - c

Nessa relação, u t - c é a função degrau:

u t - c = 0 ,         t < c 1 ,           t ≥ c

Se você quiser ver isso em detalhe, dá uma olhadinha nos resumos do RespondeAí.

Observe que

L - 1 e - s s - 1 = L - 1 e - s ⋅ 1 s - 1 = L - 1 e - s ⋅ L e t

Desta forma, f t = e t e c = 1 , de modo que

L - 1 e - s s - 1 = f t - 1   u t - 1 = e t - 1   u t - 1

Da mesma forma, com f t = e - t e c = 1 :

L - 1 e - s s + 1 = L - 1 e - s ⋅ 1 s + 1 = L - 1 e - s ⋅ L e - t = e - t - 1 u t - 1

Agora podemos escrever x t :

x t = L - 1 L x t = 1 2 e t - 1 2 e - t + a 2 ⋅ e t - 1   u t - 1 - a 2 ⋅ e - t - 1 u t - 1

Juntando os termos

x t = e t - e - t 2 + a ⋅ e t - 1 - e - t - 1 2   u t - 1

Passo 4

No item (b), o problema pede para usarmos o software Mathematica para resolver a EDO com condições iniciais x 0 = 0 e x ' 0 = 1 . O Mathematica é um software pago, mas existe uma versão gratuita dele disponível na internet com algumas funções chamada Wolfram. A seguir dou o passo a passo de como você pode resolver esse problema por lá.

Primeiro entre no site wolframalpha.com. Em seguida, procure a opção “Differential equations” na primeira coluna de opções. Em seguida, clique na opção “specify initial values”. Daí, apague a equação escrita e escreva exatamente como na figura a seguir:

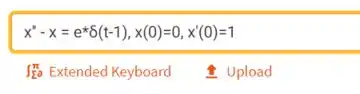
É importante que você escreva exatamente dessa forma para o programa entender direitinho. Para adicionar o δ , clique em “extended keyboard”. A solução dada pelo programa foi

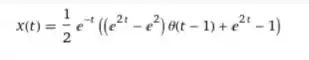
O programa chama a função degrau de θ . O gráfico fornecido foi

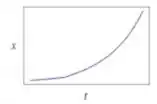
Com isso finalizamos o problema 😉.

Resposta

x t = e t - e - t 2 + a ⋅ e t - 1 - e - t - 1 2   u t - 1

Exercícios de Livros Relacionados

Considere a função p definida por: p ( t )=t ,0 ≤ t1 , 2 - t ,1 ≤ t2 ; p ( t + 2 ) = p ( t ) Esboce o gráfico de y = p(t).Encontre ℒ { p ( t ) } , notando que p é a extensão periódica da função h no P
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 1 9 s 2 - 12 s + 3
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 2 s + 1 4 s 2 + 4 s + 5
Use o resultado do Problema 34 para encontrar a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t ) =- 1 ,1 ≤ t2 ; f ( t + 2 )=f ( t ) função f ( t )
Encontre a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t )=0 ,1 ≤ t2 f ( t )=1 ,2 ≤ t3 f ( t )=0 ,t ≥ 3