Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO de 2ª Ordem com Coeficientes Constantes – Função Degrau e Delta de Dirac

Ver Teoria
Exercício 211234567891011121314151617181920222324252627282930313233343536373839404142434445464748495051525354555657

Enunciado

Transformada de Laplace, Solução de PVI para EDO por Laplace, Função degrau

Resolver o problema de valores iniciais:

y ' ' t + 4 y t = g ( t ) y 0 = y ' 0 = 0              

g t = 0       s e       0 ≤ t < 3 2         s e       3 ≤ t < 5 0         s e       t > 5                  

Passo 1

Antes de tudo, precisamos escrever essa função g ( t ) como função degrau, para isso vamos fazer seu esboço:

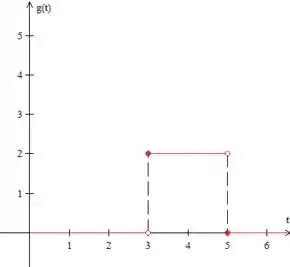
Isso é o mesmo que:

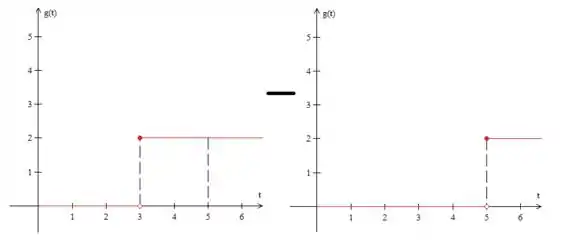
Temos, então,

g t = 2 u 3 t - 2 u 5 ( t )

Passo 2

Vamos aplicar a Transformada de Laplace à EDO.Temos o seguinte:

L y ' ' + 4 y ( s ) = L [ g ( t ) ] ( s )

L y ' ' s + 4 L y s = 2 L [ u 3 - u 5 ] ( s )

Sabemos que

L u c t s = e - s c s

Então, temos:

L y ' ' s + 4 L y s = 2 e - 3 s - e - 5 s s

Agora vamos aplicar aquela propriedade da Transformada da derivada:

L y ' ' s = s 2 L y s - s y 0 - y ´ ( 0 )

Substituindo na equação, temos:

s 2 L y s - s y 0 - y ´ 0 + 4 L y s = 2 ( e - 3 s - e - 5 s ) s

Passo 3

Vamos, então, substituir os valores iniciais e isolar L y ( s )

Como y 0 = 0   e   y ' 0 = 0 , temos:

s 2 L y s + 4 L y s = 2 ( e - 3 s - e - 5 s ) s

( s 2 + 4 ) L y s = 2 ( e - 3 s - e - 5 s ) s

L y s = 2 ( e - 3 s - e - 5 s ) 1 s ( s 2 + 4 )

Passo 4

Agora vamos decompor aquela fração em frações parciais.

  1. Fatorar o denominador

    2. Bom, esse denominador já está fotorado, não é? O termo ( s 2 + 4 ) não possui raízes reais, não temos muito o que fazer: nossas frações parciais terão esses mesmos termos no denominador.

  2. Igualar a fração à soma de frações com denominadores iguais aos termos que encontramos. Como assim? Veja:

    3. 1 s ( s 2 + 4 ) = a s + b s + c ( s 2 + 4 )

    Importante: o numerador dessas frações que criamos sempre deve ter grau menor que o fator do denominador em uma unidade.

  3. Fazer o MMC dessas frações, juntá-las ao mesmo denominador.

    4. 1 s ( s 2 + 4 ) = a s 2 + 4 + b s + c s s ( s 2 + 4 )

  4. Agora, partindo do princípio que essas duas frações são iguais, vamos encontrar os coeficientes das frações parciais.

    5. Vamos juntar os termos pelos graus de s .

    1 s s 2 + 4 = a + b s 2 + c s + 4 a s s 2 + 4

    Como o denominador já é o mesmo, temos

    1 = a + b s 2 + c s + 4 a

    Vamos igualar cada coeficiente das potências de s na esquerda e na direita. Como assim? Olha só:

    a + b = 0       →       a = - b c = 0                                                                     4 a = 1       →         a = 1 / 4      

    b = - 1 / 4

  5. Agora que já temos os coeficientes basta reescrever as frações que criamos.

1 s ( s 2 + 4 ) = 1 / 4 s + - s / 4 ( s 2 + 4 )

Então, temos:

L y s = 2 e - 3 s - e - 5 s 1 / 4 s - s / 4 s 2 + 4

Passo 5

Agora que já temos as frações parciais, precisamos reconhecer a função y pela sua transformada. Vamos reescrever essa expressão de L [ y ] para facilitar nossa vida:

L y s = e - 3 s 2 1 s - s s 2 + 4 - e - 5 s 2 1 s - s s 2 + 4

Você já vai entender porque escrevemos assim! Temos o seguinte:

s s 2 + 4 = L cos ⁡ 2 t ( s )

1 s = L 1 ( s )

Beleza? Então vamos substituir isso na nossa expressão:

L y s = e - 3 s 2 L 1 - cos ⁡ 2 t ( s ) - e - 5 s 2 L 1 - cos ⁡ 2 t ( s )

Sobrou essa exponencial fora da transformada, não é? Vamos usar então essa fórmula aqui:

L u c ( t ) f t - c s = e - c s L f t ( s )

Que tem exatamente o que queremos. Assim, vamos conseguir colocar tudo dentro de “ L ”, para poder reconhecer a função y . Aplicando a fórmula, temos:

1 2 L u 3 ( t ) f t - 3 s = e - 3 s 2 L 1 - cos ⁡ 2 t ( s )

1 2 L u 3 t - u 3 t cos ⁡ ( 2 t - 6 ) s = e - 3 s 2 L 1 - cos ⁡ 2 t ( s )

Para a segunda parte:

1 2 L u 5 ( t ) f t - 5 s = e - 5 s 2 L 1 - cos ⁡ 2 t ( s )

1 2 L u 5 t - u 5 t cos ⁡ ( 2 t - 10 ) s = e - 5 s 2 L 1 - cos ⁡ 2 t ( s )

Substituindo essas duas expressões:

L y s = 1 2 L u 3 t - u 3 t cos ⁡ ( 2 t - 6 ) s - 1 2 L u 5 t - u 5 t cos ⁡ ( 2 t - 10 ) s

y x = u 3 t - u 5 t 2 + u 5 t 2 cos ⁡ 2 t - 10 - u 3 t 2 cos ⁡ ( 2 t - 6 )

Resposta

y t = u 3 t - u 5 t 2 + u 5 t 2 cos ⁡ 2 t - 10 - u 3 t 2 cos ⁡ ( 2 t - 6 )

Exercícios de Livros Relacionados

Considere a função p definida por: p ( t )=t ,0 ≤ t1 , 2 - t ,1 ≤ t2 ; p ( t + 2 ) = p ( t ) Esboce o gráfico de y = p(t).Encontre ℒ { p ( t ) } , notando que p é a extensão periódica da função h no P
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 1 9 s 2 - 12 s + 3
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 2 s + 1 4 s 2 + 4 s + 5
Use o resultado do Problema 34 para encontrar a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t ) =- 1 ,1 ≤ t2 ; f ( t + 2 )=f ( t ) função f ( t )
Encontre a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t )=0 ,1 ≤ t2 f ( t )=1 ,2 ≤ t3 f ( t )=0 ,t ≥ 3