Duas partículas executam movimentos harmônicos simples de mesma amplitude (A) e mesmo período (T) ao longo de retas paralelas muito próximas. Existe uma diferença de fase de entre os movimentos. Considere que a partícula 2 está atrasada em relação à primeira e que a posição da primeira é descrita por
a) Escreva a posição da segunda partícula, .
Faça (no caderno de respostas) o gráfico das posições e das partículas em função do tempo para o intervalo (indique, os zeros e os pontos de máximo e mínimo das
funções).
b) Determine a distância entre as partículas (em termos de A) quando a partícula mais atrasada passar pelo ponto de maior deslocamento.
c) Determine, em função de A, em que posições as partículas passam uma pela outra.
d) Determine, em função de A e T, as velocidades das partículas nessas posições do item (c).
Passo 1
a) Primeiro precisamos lembrar que equação geral que descreve movimentos harmônicos simples é
Onde A é a amplitude, é a constante de fase e é a frequência angular. Onde
Para a partícula 1, temos que , e para a partícula 2, .
Como a questão diz que a partícula 2 está ATRASADA em relação a 1, então concluímos que .
Podemos escrever que:
Passo 2
Precisamos esboçar os gráficos de e para .
Primeiro para :
Para :
Os zeros da função ocorrem quando:
Os pontos de máximo ocorrem quando:
Os pontos de mínimo,
Passo 3
Para agora:
Para ,
Os zeros:
Os máximos:
Os mínimos:
Juntando todas essas informações num gráfico ().
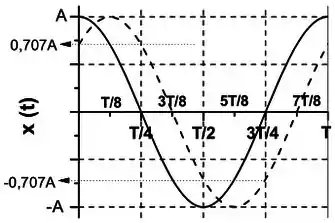
Passo 4
b) Quando a partícula 2 passar pelo ponto de maior deslocamento:
A distância entre as partículas será:
Passo 5
c) As posições em que as partículas passam uma pela outra. Se olhar no gráfico, as curvas se encontram em 2 pontos, um com deslocamento positivo e outro negativo.
Aqui, temos que levar em consideração que . Então
Com o sinal de mais não encontraremos o resultado. Mas com o sinal de menos, chegaremos em:
Então a posição em que as partículas passarão uma pela outra será (basta substituir em 1 ou em 2):
O outro ponto em que as curvas se encontram será, por simetria:
Mas se você quiser calcular pra ter certeza, você pode chegar nesse resultado usando o fato de que . Então, usando a mesma equação de antes, só que adicionando um termo no lado direito:
Passo 6
d) Calcular as velocidades nos pontos do item (c): .
Basta lembrar que a velocidade é a derivada temporal da posição, então:
Já para
No outro ponto de interseção, , os módulos das velocidades vão ser iguais, mas seus sinais estarão opostos. Então,
Resposta
a)
b)
c)
d)
.