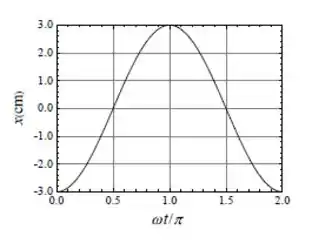
A figura ao lado mostra o gráfico da posição em função do tempo de um oscilador harmônico simples, constituído de um sistema massa-mola com constante elástica . Determine:
- a velocidade inicial da massa em
- o valor máximo de sua energia cinética em joules.
Passo 1
Galera no gráfico não temos informações da velocidade, mas temos informações sobre o deslocamento em função do tempo. Logo, conseguimos através disso obter a velocidade inicial da massa no instante .
Sabemos que a derivada da posição em relação ao tempo é a velocidade, logo:
Portanto a derivada:
Passo 2
A energia potencial máxima é dada por:
E como no oscilador harmônico simples a energia potencial máxima é igual à energia cinética máxima, a energia cinética máxima também será igual a .
Resposta
a) 0
b) 27 J
Exercícios de Livros Relacionados
Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
Recentemente tornou-se possível “pesar” moléculas de DNA medindo a influência de sua massa sobre um nano-oscilador. A figura mostra uma haste fina, retangular e nanométrica, escavada em silicone (dens
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad