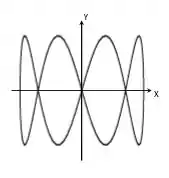
A figura de Lissajous abaixo descreve o movimento de uma massa sujeita a duas forças restauradoras perpendiculares, independentes, e . Qual é a razão entre as constantes destas forças restauradoras?
2
Passo 1
Como as forças são independentes, cada uma é responsável pelo movimento da massa naquela direção. Então o movimento em é devido à força , e em é devido à força .
Então haverá períodos para esse movimento em cada direção, que chamaremos de e de .
Agora, imagina uma coisa aqui comigo. Se você olhasse a massa se deslocando só no eixo x, você iria vê-la ir e voltar de uma extremidade à outra, numa linha horizontal, em cima do eixo x.
Se você visse o movimento só no eixo y, veria a massa se deslocar de um máximo a um mínimo de amplitude, em cima do eixo y.
Como nós temos força nas duas direções o movimento fica essa coisa esquisita da figura.
Agora, se você olhasse a massa se deslocando só no eixo x, em um período ela iria de uma extremidade à outra, e voltaria até a extremidade inicial. Se você contar quantas vezes a massa fez uma oscilação completa no eixo y, enquanto completava um período no eixo x, vai ver que foram 4 vezes (4 cristas, 4 vales). Disso a gente consegue concluir que:
Lembrando que
Assim temos que:
Resposta
Alternativa