Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição e Fase do MHS

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738

Enunciado

Um oscilador harmônico simples é formado por um bloco preso a uma mola com k = 200   N / m . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de 0,20   m . A figura ao lado representa o gráfico da velocidade v do bloco em função do tempo t. Considere π 2 ≈ 10 . Cuidado com os sinais!

Dados: x ( t )   =   x m cos ⁡ ( ω t + Φ )

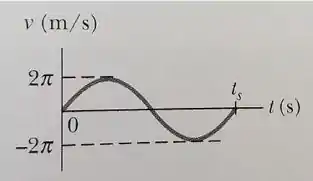
a) Qual é o período do MHS?

b) Qual é a massa do bloco?

c) Qual o deslocamento do bloco no instante t = 0 ?

d) Qual é a aceleração do bloco no instante t = 0,10   s ?

Passo 1

Ele deu pra gente que:

x ( t )   =   x m cos ⁡ ( ω t + Φ )

E essa é a posição! Mas como o gráfico é de velocidade, vamos derivar essa fórmula da posição pra encontrar a velocidade, que é o que tá no gráfico.

Adoro derivar! (É brincs.) Mas então, derivando:

x ˙ t =   - x m ω sin ⁡ ( ω t + Φ )

E olhando no gráfico, vemos que a velocidade máxima é 2 π . Então:

x m ω = 2 π

E ele deu a amplitude do movimento, que é x m :

x m = 0,2   m

0,2 × ω = 2 π

ω = 10 π

Com ω podemos calcular o período:

T = 2 π ω = 2 π 10 π

T = 0,2   s

Passo 2

b) Nós já achamos a frequência angular e temos o k da mola! Podemos fazer então:

ω 2 = k m

( 10 π ) 2 = 200 m

m = 200 ( 10 π ) 2

Como ele mandou considerar que π 2 = 10 :

m = 200 1000

m = 0,2   k g

Passo 3

c) O deslocamento no instante zero vai ser:

x ( 0 )   =   x m cos ⁡ ( Φ )

x ( 0 )   =   0,2 cos ⁡ ( Φ )

Opa! Mas não temos Φ . Vamos achar então.

Vou usar o gráfico. Repare que a velocidade máxima, igual a 2 π , acontece em um tempo que é igual a ¼ do período. E como o período nós sabemos, podemos fazer:

x ˙ T / 4 =   - x m ω sin ⁡ ω T 4 + Φ

E trocando T por 0,2 s:

x ˙ 0,05 =   - x m ω sin ⁡ 0,05 ω + Φ

Trocando os valores conhecidos:

x ˙ 0,05 =   - 0,2 × 10 π sin ⁡ 0,05 × 10 π + Φ

x ˙ 0,05 =   - 2 π sin ⁡ 0,5 π + Φ

E x ˙ 0,05 é um máximo, então:

2 π =   - 2 π sin ⁡ 0,5 π + Φ

sin ⁡ 0,5 π + Φ = - 1

π 2 + Φ = 3 π 2

Φ = π

Passo 4

Então:

x ( t )   =   x m cos ⁡ ( ω t + Φ )

x ( t )   =   0,2 cos ⁡ ( 10 π t + π )

Vamos calcular x(0):

x ( 0 )   =   0,2 cos ⁡ ( π )

x 0 = -   0,2   m

Passo 5

d) A velocidade vai ser:

x ˙ t =   - x m ω sin ⁡ ( ω t + Φ )

Trocando os valores:

x ˙ t =   - 2 π sin ⁡ ( 10 π t + π )

Para achar a aceleração, derivamos mais uma vez:

x ¨ t =   - 2 π × 10 π cos ⁡ ( 10 π t + π )

x ¨ t =   - 20 π 2 cos ⁡ ( 10 π t + π )

Como π 2 = 10 :

x ¨ t =   - 200 cos ⁡ ( 10 π t + π )

No instante 0,1 então:

x ¨ 0,1 =   - 200 cos ⁡ 10 π × 0,1 + π

x ¨ 0,1 =   - 200 cos ⁡ π + π = - 200 cos ⁡ 2 π

x ¨ 0,1 = - 200   m s 2

Resposta

a) T = 0,2   s

b) m = 0,2   k g

c) x 0 = -   0,2   m

d) x ¨ 0,1 = - 200   m s 2

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
Recentemente tornou-se possível “pesar” moléculas de DNA medindo a influência de sua massa sobre um nano-oscilador. A figura mostra uma haste fina, retangular e nanométrica, escavada em silicone (dens
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad