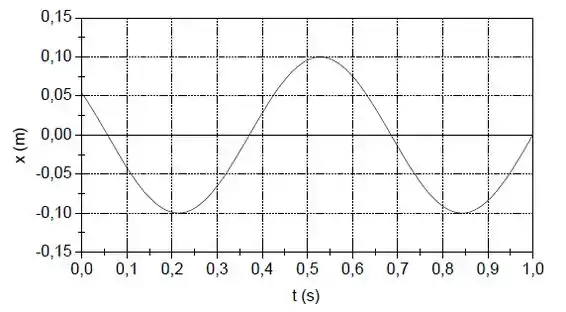
O gráfico abaixo mostra a oscilação horizontal de um bloco de massa 0,20 kg preso a uma mola ideal.
a) Qual a constante elástica da mola?
b) Escreva a equação que descreve x(t).
c) Qual é o módulo da velocidade do bloco ao passar pela posição de equilíbrio?
Passo 1
a) Então, lembra que a gente tem uma fórmula pro período? Ela é:
Bom, já temos a massa. Então se acharmos o período encontramos a constante k da mola! Show, então vamos em busca do período.
Dá uma olhada no gráfico.
Concorda comigo que um período vai ser 6 quadradinhos mais 1/3 de quadradinho? Mais ou menos. Então:
Trocando isso na fórmula de antes:
Passo 2
b) Bom, bloco preso a uma mola sem amortecimento é sempre MHS. E você lembra da posição do MHS? Ela é:
E como o gráfico que ele dá é exatamente de x(t) a gente vai tirar alguns valores de lá.
Dá pra ver pelo gráfico que a amplitude é 0,1 m. Então:
E pelo valor que achamos do período, conseguimos achar a frequência angular. Porque:
Então:
Beleza! Então podemos escrever:
Só falta ! E como vamos achar ? Vamos usar a condição inicial. No instante vamos ter:
E pelo gráfico, . Então:
Passo 3
c) Na letra c ele pede a velocidade do bloco ao passar pela posição de equilíbrio.
Bom, quando o bloco passa pelo equilíbrio a velocidade dele é máxima! Porque a mola tá completamente relaxada, então o bloco só tem energia cinética e ela será igual à energia total.
Então se a gente achar a velocidade máxima a gente acha a velocidade do bloco ao passar pela posição de equilíbrio.
Lembra que a derivada da posição é a velocidade? Então vamos derivar a posição:
E aí, qual vai ser a velocidade máxima?
A velocidade máxima vai ser igual à amplitude da velocidade. Ou seja:
Resposta
a)
b)
c)