Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição e Fase do MHS

Ver Teoria
Exercício 2412345678910111213141516171819202122232526272829303132333435363738

Enunciado

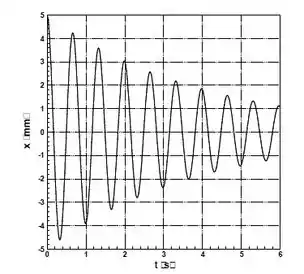
Um oscilador harmônico fracamente amortecido é descrito pela equação m x ˙ ˙ = - k x - ρ x ˙ e a posição da massa em função do tempo é mostrada no gráfico abaixo. Para uma massa m = 1 k g , os valores de k e ρ mais apropriados para este oscilador (dica: l n 5 ≅ 1.6 ; l n 3 ≅ 1.1 ;   π 2 ≈ 10 ) são:

  1. k   =   50 N m   e   r   =   5 k g s .
  2. k   =   50 N m   e   r   =   0 ,   5 k g s .
  3. k   =   10 N m   e   r   =   10 k g s .
  4. k   =   100 N m   e     r   =   5 k g s .
  5. k   =   90 N m   e     r   =   0 ,   5 k g s .

Passo 1

Do gráfico vemos que o regime de amortecimento é o sub-crítico. Logo, a solução x ( t ) é da forma

x t = e - γ t 2 [ acos ⁡ ω t + b s e n ω t = A e - γ t 2 cos ⁡ ( ω t + ϕ )

Com

ω = ω 0 2 - γ 2 4

Passo 2

Vemos também do gráfico que a amplitude da oscilação em t   =   2 s é 3 / 5 da correspondente amplitude em t   =   0 . Logo

A e - γ = 3 5 A

γ = ρ m = ln ⁡ 5 3 = l n 5 - l n 3 = 0,5

ρ = 0,5   k g / s

Passo 3

Também vemos do gráfico que o período das oscilações amortecidas é T   = 2 3 s , logo ω = 3 π r a d / s e, portanto

ω 2 = ω o 2 - γ 4 = k m - ρ 2 4 m 2 = 9 π 2 = 90

k = 90 N / m

Resposta

Letra E

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
Recentemente tornou-se possível “pesar” moléculas de DNA medindo a influência de sua massa sobre um nano-oscilador. A figura mostra uma haste fina, retangular e nanométrica, escavada em silicone (dens
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad