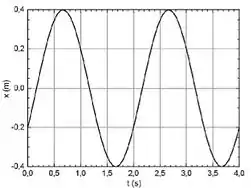
O gráfico mostra a oscilação de um bloco de massa preso a uma mola. Responder justificando:
- Qual é a constante elástica da mola?
- Qual é o módulo da velocidade do bloco ao passar pela posição de equilíbrio?
- Qual é a constante de fase?
Passo 1
Certo, vamos lá! Analisando o gráfico, temos que a amplitude do movimento que vale e o período vale .
Para acharmos a constante elástica, sabendo estes valores, basta aplicarmos a fórmula. Mas, vamos deduzí-la por energia.
Quando o bloco está na amplitude máxima, tem apenas energia elástica:
E quando está em , tem apenas energia cinética:
Como a energia do sistema se conserva, podemos dizer que:
Passo 2
Ixi, não temos a velocidade máxima. Mas espera aí, a gente sabe que para movimentos circulares, cuja dimensão característica é o raio, a velocidade vale:
Então, analogamente, para movimentos oscilatórios, onde é a dimensão característica do movimento, temos:
Passo 3
Agora sim podemos finalizar a questão substituindo os valores que já conhecemos.
Passo 4
Como só temos a força elástica atuando, a posição de equilíbrio (que é quando a força resultante é nula) é em . Neste caso, a velocidade que buscamos é, então a velocidade máxima.
Já calculamos, mas só pra confirmar, continuando com a energia, podemos voltar a usar a fórmula:
Passo 5
Vamos começar com a fórmula que a gente já sabe:
Para
Aqui temos duas possibilidades que dão cosseno igual a
Mas só uma dessas fases é o correto! Pra descobrir qual dos dois, vamos olhar pra velocidade! Isso por que lá no gráfico do enunciado dá pra ver que a velocidade inicial é positiva, já que aumenta em , beleza?
Pra achar a velocidade vamos simplesmente derivar
Em essa velocidade será
Como
E das duas opções que temos, a que dá seno negativo é
Show :D