Fala povo, tudo ok? Olha só, vamos fingir que temos uma função oscilatória cosseno qualquer tal que:

Se compararmos essa equação genérica com a física, vemos que:

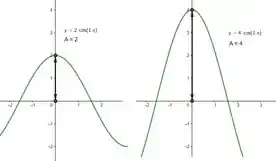
A letra representa a amplitude de oscilação. Agora pra entender , mudamos ele e vemos que:

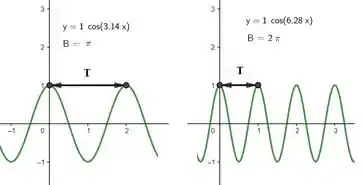
Logo o período de oscilação é:

E a frequência de oscilação será:

E por fim, vemos também que:

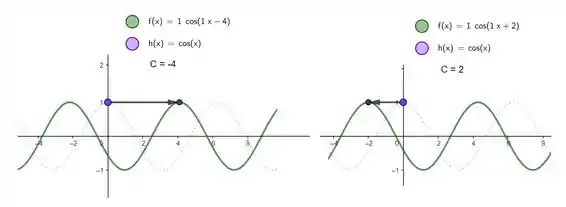
A letra vai representar nosso atraso ou adianto de fase (respectivamente)! Sendo assim, comparando matemática e física, temos:

Logo, temos:

• Amplitude de oscilação
• Período de oscilação
• Frequência de oscilação
• Adianto de fase

E isso já respondemos a letra e pegamos bastante informação sobre esse movimento. Esboçar o gráfico vai ser mais tranquilo

Passo 2

As informações todas do passo anterior são o suficiente pro esboço. Com elas, conseguimos montar :



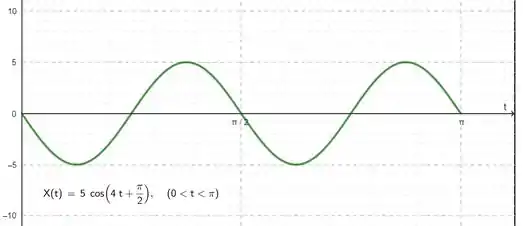
Marcando a posição nos instantes pedidos, temos:



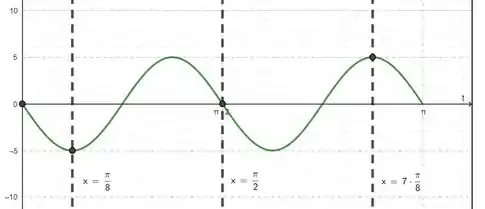
Vemos então que a posição é nos instantes e e que a posição é máxima em , alcançando o valor positivo da amplitude de oscilação e a posição é mínima em em , alcançando o valor negativo da amplitude de oscilação.

Passo 3

Pro gráfico da velocidade, temos que lembrar que:

Portanto:

Pra fazer esse gráfico galera, a ideia é quase a mesma. A amplitude mudou, mas veja que o adianto de fase, frequência e período não! Portanto, esboçando já marcando os pontos que o enunciado pede, temos:



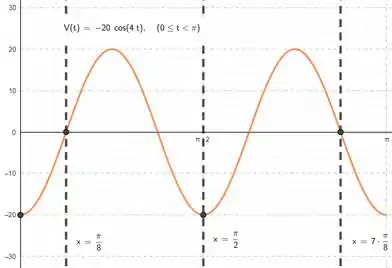
Vemos então que a velocidade é nos instantes e e que a mesma é mínima em todos os outros pontos, isto é, em e , alcançando o valor negativo da amplitude de oscilação . Nenhum dos valores de do enunciado nos fornece a velocidade máxima, que seria o valor positivo da amplitude de oscilação.

Passo 4

Galera, bora falar então do gráfico da energia cinética. Vamos lembrar que:

Como sabemos que a massa é e que a velocidade varia com o tempo, temos:

Mas como:

Podemos reescrever pra facilitar nossa vida no esboço para:

Ainda assim podemos manter a ideia de função oscilatória pra esboçar o gráfico. Nota o seguinte valera, o cosseno vai ter um valor máximo e um mínimo...

... que vai acabar implicando num valor máximo e mínimo pra também:

Então já sabemos que é uma função oscilatória mas que oscila indo de pra indo e voltando. Dessa vez a frequência ficou duas vezes maior (e o período se tornou metade) e o adianto de fase aumentou em relação a . Usando essas informações, podemos esboçar:



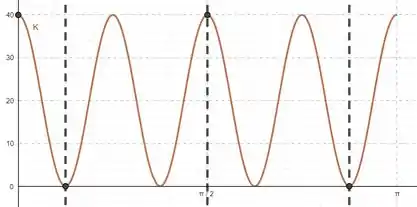
Vemos então que a energia cinética total é mínima (e nula) nos instantes e e que a mesma é máxima em todos os outros pontos, isto é, em e , alcançando o valor de .

Passo 5

Agora a gente termina tudo! Falta só o gráfico da energia mecânica total. A energia mecânica total vai ser sempre:

Onde é a soma de todas as energias potenciais. Como a oscilação é harmônica é tranquilo de assumirmos que a energia mecânica se conserva! Ou seja, quando a cinética é mínima (e nula), a potencial é máxima. E vice-versa! Ou seja, como:

O maior valor que ele pode assumir será a energia mecânica total em todos os instantes:



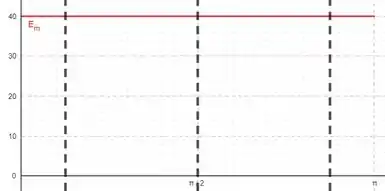
Ufa, cabamos!

Resposta

Letra a:

• Período de oscilação
• Frequência de oscilação

Letra b:

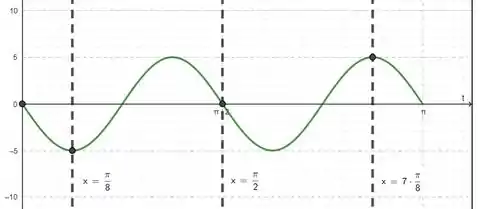
Vemos então que a posição é nos instantes e e que a posição é máxima em , alcançando o valor positivo da amplitude de oscilação e a posição é mínima em em , alcançando o valor negativo da amplitude de oscilação.

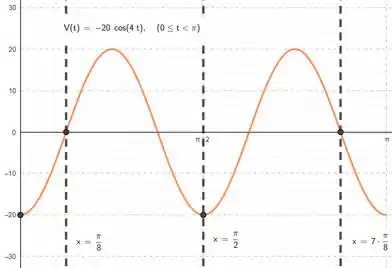
Vemos então que a velocidade é nos instantes e e que a mesma é mínima em todos os outros pontos, isto é, em e , alcançando o valor negativo da amplitude de oscilação . Nenhum dos valores de do enunciado nos fornece a velocidade máxima, que seria o valor positivo da amplitude de oscilação.

Letra c:

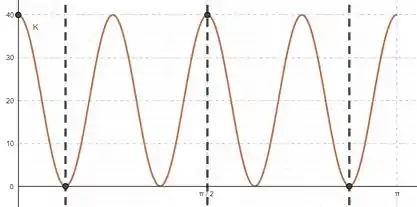
Vemos então que a energia cinética total é mínima (e nula) nos instantes e e que a mesma é máxima em todos os outros pontos, isto é, em e , alcançando o valor de .

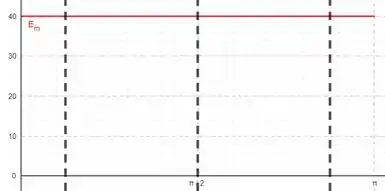
Como a energia mecânica se conserva, quando a cinética é máxima, a potencial é mínima e nula (e vice-versa). A energia cinética alcança o valor máximo de , portanto este é o valor da energia mecânica em todos os instantes.