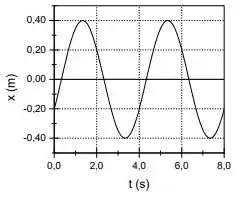
Um corpo de massa está em movimento harmônico sobre uma superfície horizontal sem atrito e preso a uma mola ideal. O gráfico mostra a posição do corpo em função do tempo . Qual é a energia cinética máxima do corpo?

(A)

(B)

(C)

(D)

(E)

A posição de uma partícula que realiza um MHS pode ser escrita como:

Agora, vamos achar os parâmetros , e .

A amplitude será:

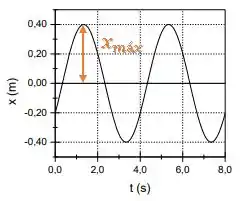
Então:

O será dado por:

Onde e o período do movimento...

O período do movimento será o tempo que o corpo leva para completar uma oscilação e voltar ao mesmo ponto de antes.

Para isso, pegamos a distância entre quaisquer pontos equivalentes (que estejam na mesma posição e com a velocidade no mesmo sentido):

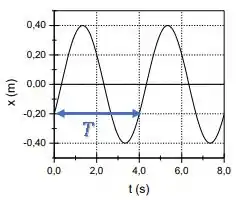
Assim, temos:

Logo:

Para achar a diferença de fase , vamos substituir os valores do ponto inicial:

Ou seja, deve ser:

Temos que tomar cuidado para não escolhermos o outro ângulo possível para que seria . Esse ângulo não está correto por mais que apresente o mesmo valor de seno que o ângulo .

Isso porque no gráfico, podemos ver que o “seno” está se aproximando de zero no trecho inicial (crescente), assim, é a única opção.

Assim, temos que a posição da partícula é:

Agora, vamos derivar para encontrar uma expressão para a velocidade:

Lembrando da regra da cadeia para a parte de dentro da função “seno”...

Já temos a expressão da velocidade.

Mas quem é a velocidade máxima da partícula?

Olha para a expressão, tá vendo que a função “cos” varia entre e ?

Então, o maior valor de velocidade que a partícula atinge é quando a função “cos” vale , portanto:

Agora, já podemos calcular a energia cinética máxima:

Então, a energia cinética máxima é aproximadamente:

Ficamos com a alternativa (a).