UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 33a
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
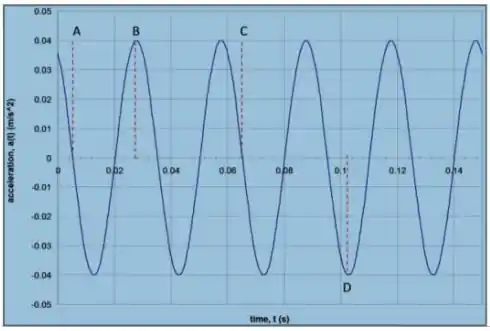
O deslocamento máximo do corpo.
Passo 1
Oiie, tudo certinho contigo?
Temos o seguinte gráfico
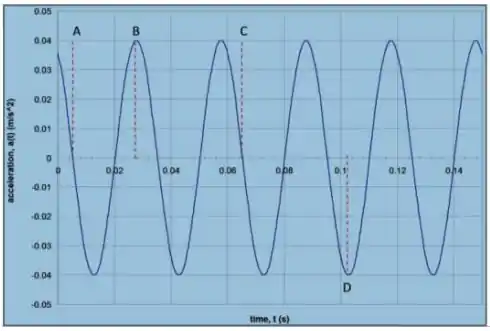
ele indica a aceleração em função do tempo de uma partícula de massa que está preso em uma mola! Ou seja, na ausência de atrito temos um movimento harmônico simples! Esta alternativa pede
O deslocamento máximo do corpo.
Ou seja, a amplitude do movimento oscilatório! Esse gráfico é da aceleração, então temos que obter uma solução da forma
ou
qual iremos escolher é uma questão das condições iniciais do nosso problema! Temos que é o deslocamento máximo (a amplitude) da oscilação, é a frequência natural de oscilação e é a fase do movimento! Eventualmente todos terão que ser encontrados! Vamos analisar isso com calma!
Passo 2
Observando o gráfico no ponto , temos que a aceleração máxima é tal que
Lembrando a segunda lei de Newton
Como temos uma massa ligada a uma mola, temos que
De forma que o deslocamento máximo é da forma
em que usei a definição
Já que não temos a constante elástica! Vamos observar o gráfico para obter a nossa frequência natural!
Passo 3
Temos que a distância entre dois picos indica o período , e como temos a relação
é o caminho mais simples que podemos seguir! O pico em está no tempo
o pico subsequente está em
Sendo assim, o período é dado por
Ou seja, a frequência natural é
Vamos finalizar essa alternativa agora!
Passo 4
Usando a frequência natural que obtemos dos dados gráficos, temos que o deslocamento máximo é
A questão foi isso! Te vejo na próxima! Tchau Tchau!