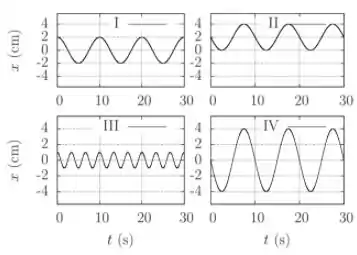
. Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA.
oscila com frequência menor que todos os restantes.
e partem de sua posição de equilíbrio em .
e oscilam com a mesma amplitude.
e oscilam com período de .
realiza oscilações por minuto.
Passo 1
Vem comigo que a gente resolve juntos esse problema!
Antes de começarmos, vamos apontar coisas sobre o oscilador harmônico e sobre o gráfico do movimento de um oscilador.
- A frequência de um oscilador é o número de oscilações que temos por segundo.
- O período de um oscilador é tempo que leva para termos um comprimento de onda. No gráfico esse valor é dado pela distância entre os picos ou entre os pontos de equilíbrio.
- Podemos identificar a amplitude no gráfico pela altura do pico contando da posição de equilíbrio.
Vamos nessa então!
Passo 2
Começando a letra .
Ela diz que oscila com frequência menor que o resto.
Mas se olharmos nos gráficos e contarmos os comprimentos de onda de cada um deles vemos que o é o que mais tem comprimentos de onda no mesmo intervalo de tempo.
Logo essa letra está errada.
Passo 3
Agora vamos ver a letra .
Ela diz que os gráficos e partem da posição de equilíbrio em .
A posição de equilíbrio é onde temos uma linha horizontal que divide o gráfico ao meio. Então olhando esses gráficos vemos que a alternativa é correta.
Passo 4
Agora vamos ver a letra .
Ele afirma que os gráficos e oscilam com a mesma amplitude.
Olhando a altura dos picos a parti da posição de equilíbrio desses gráficos temos que essa alternativa está correta.
Passo 5
Agora vamos ver a letra .
Ele diz que os gráficos , e tem um período de .
Olhando esses gráficos e usando o que temos sobre o período no passo , vemos que todos levam para ter um comprimento de onda. Logo a afirmação é verdadeira.
Passo 6
Agora vamos ver a letra .
Essa alternativa diz que o faz oscilações em um minuto.
Levando em conta que uma oscilação representa um comprimento de onda e olhando o gráfico vemos que nos primeiros temos três comprimentos de onda, logo três oscilações.
Então em temos oscilações.
Essa alternativa também está correta.
Com isso temos que a única errada é a letra .
Resposta
oscila com frequência menor que todos os restantes.