Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição e Fase do MHS

Ver Teoria
Exercício 8123456791011121314151617181920212223242526272829303132333435363738

Enunciado

MHS

A figura abaixo mostra um gráfico de posição v s tempo de um oscilador harmônico simples.

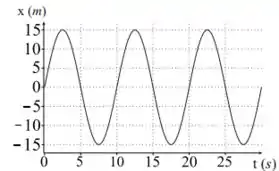
A função x ( t ) que melhor descreve o movimento do oscilador harmônico mostrado no gráfico acima é dada por:

  1. x t = 15 cos ⁡ 0,1 t + π 2 .
  2. x t = 15 cos ⁡ 0,1 t - π 2 .
  3. x t = 15 cos ⁡ 0,2 π t + π 2 .
  4. x t = 15 cos ⁡ 0,2 π t - π 2 .
  5. x t = 30 cos ⁡ 0,1 t + π 2 .
  6. x t = 30 cos ⁡ 0,1 t - π 2 .
  7. x t = 30 cos ⁡ 0,2 π t + π 2 .

Passo 1

A função da posição do MHS tem a forma:

x t = A c o s ω t + φ

Então vamos descobrir cada constante usando o gráfico.

Passo 2

A amplitude é o máximo afastamento da origem, ou seja, o máximo de x t . Pelo gráfico, você pode ver que ela vale 15 m :

A = 15 m

Passo 3

Pra achar ω é melhor a gente achar o período T e depois calculá-la. Pelo gráfico, você consegue perceber que cada pico, cada vale, ou cada x t = 0 , se repete a cada 10 s . Então:

T = 10 s

Usando a fórmula:

ω = 2 π T = 2 π 10 = 0,2 π

Então a nossa fórmula já tá assim:

x t = 15 c o s ⁡ ( 0,2 π t + φ )

Passo 4

Falta descobrir o φ . Como? Bom, vamos pegar o valor da função em t = 0 . Assim:

t = 0 → x 0 = A c o s 0 + φ = A c o s φ = 0

∴

cos ⁡ φ = 0   → φ = ( 2 n + 1 ) π 2

Ou seja, um múltiplo impar de π 2 .

Passo 5

Uma forma de se descobrir quem é essa fase é calculando a derivada de x t . Olhe para o gráfico, a derivada de x ( t ) vai representar o ângulo da reta tangente ao gráfico em cada ponto, não é mesmo?

Por que? Ora, porque é um gráfico de t   v s   x ( t ) .

Então vamos usar esse fato pra descobrir quem é a fase. Vamos lá:

d x t d t = - ω A s e n ( ω t + φ )

Agora vamos calcular o valor disso em t = 0 :

d x 0 d t = - ω A s e n ( φ )

Agora olhe no gráfico: Quando t = 0 , a derivada não é positiva? Então, olhando pra d x t d t , que tem um menos dentro da fórmula, qual o valor da fase para que , no fim, tudo fique positivo?

φ = - π 2

Certo? Vamos checar:

d x 0 d t = - ω A s e n - π 2 = - ω A . - 1 = ω A > 0

Então é isso! E a expressão completa pra x ( t ) será:

x t = 15 cos ⁡ 0,2 π t - π 2

d)

Resposta

d)

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
Recentemente tornou-se possível “pesar” moléculas de DNA medindo a influência de sua massa sobre um nano-oscilador. A figura mostra uma haste fina, retangular e nanométrica, escavada em silicone (dens
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad