Listas de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 3 da UTFPR - Integrais de Linha

Calcule a integral de linha, onde é a curva dada.

Calcule a integral de linha, onde é a curva dada.

Calcule a integral de linha , onde é dada pela função vetorial .

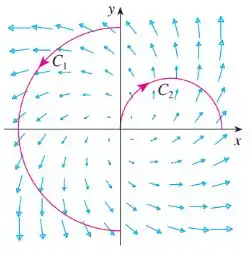
A figura mostra um campo vetorial e duas curvas, e . As integrais de linha de sobre e são positivas, negativas ou nulas? Explique.

Calcule a integral de linha , onde é dada pela função vetorial .

Calcule a integral de linha , onde é dada pela função vetorial .

Calcule a integral de linha, onde é a curva dada.

Calcule a integral de linha, onde é a curva dada.

Calcule a integral de linha, onde é a curva dada.

(Cap.16.2 - Ex.39) Determine o trabalho realizado pelo campo de força sobre um objeto que se move sobre um arco da cicloide .

(Capítulo 16.2 – Exercício 40) Determine o trabalho realizado pelo campo de força em uma partícula que se move sobre a parábola de a .

(Cap.16.2 - Exercício 42) A força exercida pela carga elétrica colocada na origem sobre uma partícula carregada em um ponto com vetor posição é , onde é uma constante (veja o Exemplo da seção ). Encontre o trabalho feito quando a partícula se move ao longo de uma linha reta de a .

(Cap.16.3 - Exercício 3) Determine se é ou não um campo vetorial conservador. Se for, determine uma função tal que

(Cap.16.3 - Exercício 5) Determine se é ou não um campo vetorial conservador. Se for, determine uma função tal que .

(Cap.16.3 - Exercício 7) Determine se é ou não um campo vetorial conservativo. Se for, determine uma função tal que

(Cap.16.3 - Exercício 12) (a) Determine uma função tal que e (b) Use a parte (a) para calcular sobre a curva dada.

é o arco da parábola de a

(Capítulo 16.3 – Exercício 15)

(a) Determine uma função tal que e (b)Use a parte (a) para calcular sobre a curva dada.

é o segmento de reta de

(Cap.16.3 - Exercício 18) (a) Determine uma função tal que e (b) use a parte (a) para calcular sobre a curva dada.

,

(Cap.16.3 - Exercício 23) Determine o trabalho realizado pelo campo de força ao mover um objeto de para .

(Cap.16.3 - Exercício 35) Seja

(a) Mostre que .

(b) Mostre que não é independente do caminho. [Dica: Calcule e onde e são as metades superior e inferior do círculo de a .] Isso contradiz o Teorema ?

(Cap.16.4 - Exercício 1) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

é o círculo com centro na origem e raio

(Cap.16.4 - Exercício 2) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

é o retângulo com vértices

(Cap.16.4 - Exercício 3) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

é o triângulo com vértices e

(Cap.16.4 - Exercício 4) Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

(Capítulo 16.4 – Exercício 5) Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

,

é o triângulo de vértices

(Cap.16.4 - Exercício 7) Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

é o limite da região englobada pelas parábolas e

(Cap.16.4 - Exercício 10) Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.

(Cap.16.4 - Exercício 11) Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)

, é o triângulo de

(Cap.16.4 - Exercício 28) Calcule , onde e é a fronteira positivamente orientada de uma região que tem área 6.