Listas de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 3 da UTFPR - Funções Vetoriais

(Capítulo 13.1 – Exercício 5) Calcule os limites.

(Capítulo 13.2 – Exercício 10)

Determine a derivada da função vetorial

(Capítulo 13.1 – Exercício 47) Se dois objetos viajam pelo espaço ao longo de duas curvas diferentes, é sempre importante saber se eles vão colidir. (Será que um míssil atingiu seu alvo em movimento? Vão se colidir duas aeronaves?) As curvas podem se interceptar, mas precisamos saber se os objetos estarão na mesma posição no mesmo instante. Suponha que as trajetórias de duas partículas sejam dadas pelas seguintes funções vetoriais

Para

As partículas colidem?

(Capítulo 13.1 – Exercício 3) Calcule os limites.

(Capítulo 13.2 – Exercício 23)

Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado.

(Capítulo 13.1 – Exercício 1) Determine o domínio das funções vetoriais.

(Capítulo 13.1 – Exercício 44) Determine a função vetorial que representa a curva obtida pela interseção das duas superfícies.

O semielipsoide e o cilindro

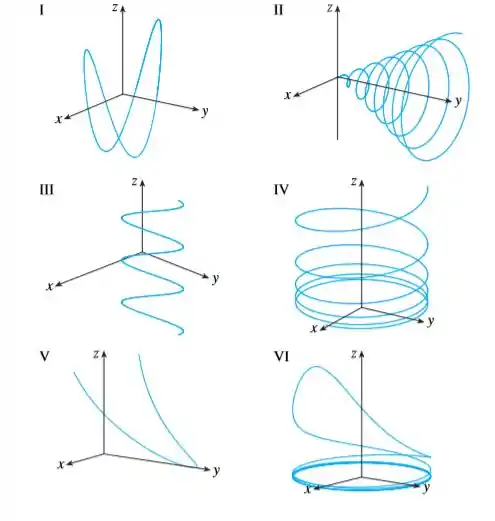
(Capítulo 13.1 – Exercício 21) Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de I–VI). Justifique sua escolha.

(Capítulo 13.1 – Exercício 40) Determine a função vetorial que representa a curva obtida pela intersecção das duas superfícies.

O cilindro de e a superfície

(Capítulo 13.1 – Exercício 41) Determine a função vetorial que representa a curva obtida pela intersecção das duas superfícies.

O cone e o plano

(Capítulo 13.1 – Exercício 42) Determine a função vetorial que representa a curva obtida pela intersecção das duas superfícies.

O paraboloide e o cilindro parabólico

(Capítulo 13.2 – Exercício 17)

Determine o vetor tangente unitário T(t) no ponto com valor de parâmetro dado t.

(Capítulo 13.1 – Exercício 7) Esboce o gráfico da curva cuja equação vetorial é dada. Indique

com setas a direção na qual o parâmetro t cresce.

(Capítulo 13.1 – Exercício 14) Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce.

(Capítulo 13.1 – Exercício 9) Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce.

(Capítulo 13.2 – Exercício 3)

(a) Esboce o gráfico da curva plana com equação vetorial dada.

(b) Determine r’(t).

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

(Capítulo 13.2 – Exercício 4)

(a) Esboce o gráfico da curva plana com a equação vetorial dada.

(b) Encontre r’(t)

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

(Capítulo 13.2 – Exercício 2)

(a) Faça um esboço grande da curva descrita pela função vetorial , e desenhe os vetores e .

(b) Desenhe o vetor começando em (1, 1) e compare com o vetor

Explique porque esses vetores estão tão próximos um do outro tanto em módulo quanto em direção e sentido.

(Capítulo 13.2 – Exercício 5)

(a) Esboce o gráfico da curva plana com equação vetorial dada.

(b) Determine r’(t).

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

(Cap. 13.2 - Ex. 24) Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado.

(Cap. 13.2 - Ex. 27) Encontre uma equação para a reta tangente à curva de intersecção dos cilindros e no ponto .

(Cap. 13.2 - Ex. 29)Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.

(Cap. 13.2 - Ex. 32) (a) Determine o ponto de intersecção das retas tangentes à curva

nos pontos e .

(b) Ilustre traçando o gráfico da curva e ambas as tangentes.

(Cap. 13.2 - Ex. 34) Em que ponto as curvas e se cruzam? Determine o ângulo de intersecção destas, com precisão de um grau.

(Cap. 13.3 - Ex. 2)Determine o comprimento da curva dada.

(Capítulo 13.2 – Exercício 36) Calcule a integral.

(Capítulo 13.3 – Exercício 3) Determine o comprimento da curva dada.

(Cap. 13.2 – Ex.49) Determine , onde , e .

(Cap. 13.3 - Ex. 4) Determine o comprimento da curva dada.

(Cap. 13.3 - Ex. 5) Determine o comprimento da curva dada.

(Cap. 13.3 - Ex. 11) Seja a curva de intersecção do cilindro parabólico e da superfície . Encontre o comprimento exato de da origem até o ponto (6, 18, 36).

(Cap. 13.3 - Ex. 13) Reparametrize a curva com relação ao comprimento de arco medido a partir do ponto onde na direção crescente de .

(Cap. 13.3 - Ex. 14) Reparametrize a curva com relação ao comprimento de arco medido a partir do ponto onde na direção crescente de .

(Capítulo 13.3 – Exercício 17)

(a) Determine os vetores tangente e normal unitários e

(b) Utilize a Fórmula 9 para encontrar a curvatura.

(Cap. 13.3 - Ex. 49) Determine as equações dos planos normal e osculador da curva no ponto indicado.

(Cap. 13.3 - Ex. 50) Determine as equações dos planos normal e osculador da curva no ponto indicado.

(Capítulo 13.4 – Exercício 4) Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.

(Cap. 13.4 - Ex. 3) Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.

(Cap. 13.4 - Ex. 15) Determine os vetores velocidade e posição de uma partícula, dadas a sua aceleração, velocidade e posição iniciais.

(Cap. 13.4 - Ex. 21) Uma força com magnitude atua diretamente para cima do plano em um objeto com massa . O objeto começa na origem com velocidade inicial . Encontre sua função posição e sua velocidade escalar no instante .

(Capítulo 13.1 – Exercício 6) Calcule os limites.