Listas de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 3 da UTFPR - Integrais de Superfícies

(Cap.16.7- Exercício 9) Calcule a integral de superfície.

S é a parte do plano que está acima do retângulo

(Cap. 16.7 - Exercício 10) Calcule a integral de superfície.

S é a parte do plano que está no primeiro octante.

(Cap. 16.7 - Exercício 5) Calcule a integral de superfície.

S é o paralelogramo com equações paramétricas ,

(Cap.16.7 - Exercício 8) Calcule a integral de superfície.

S é a superfície com equação vetorial.

(Cap.16.7 - Exercício 7) Calcule a integral de superfície.

S é o helicoide com equação vetorial

(Cap 16.7 - Exercício 17) Calcule a integral de superfície.

é o hemisfério

(Cap. 16.7 - Exercício 13) Calcule a integral de superfície.

é a parte do cone que está entre os planos e

(Cap. 16.7- Exercício 16) Calcule a integral de superfície.

é a parte da esfera que está dentro do cilindro e acima do plano .

(Capítulo 16.7 – Exercício 21) Avalie a integral de superfície para o campo vetorial dado e a superfície orientada . Em outras palavras, localize o fluxo de através de . Para superfícies fechadas, use a orientação (para o exterior) positiva.

é o paralelogramo do Exercício 5 com orientação ascendente.

Use o teorema de Stokes para calcular .

, S é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices , com orientação para fora. (Sugestão: use a equação .)

(Cap. 16.7 – Exercício 20) Calcule a integral de superfície.

é a parte do cilindro entre os planos e , juntamente com os discos inferior e superior.

(Capítulo 16.7 – Exercício 23) Avalie a integral de superfície para o campo vetorial dado e a superfície orientada . Em outras palavras, localize o fluxo de através de. Para superfícies fechadas, use a orientação (para o exterior) positiva.

S é a parte do paraboloide que está acima do quadrado e com orientação ascendente

(Capítulo 16.7 – Exercício 25) Avalie a integral de superfície para o campo vetorial dado e a superfície orientada . Em outras palavras, localize o fluxo de através de. Para superfícies fechadas, use a orientação (para o exterior) positiva.

“é a parte da esferano primeiro octante, com orientação para a origem.”

(Cap.16.8 - Exercício 3) Use o teorema de Stokes para calcular .

, S é a parte do parabolóide que está dentro do cilindro , com orientação ascendente.

(Cap 16.7- Exercício 18) Calcule a integral de superfície.

é o limite da região delimitada pelo cilindro e pelos planos e

(Cap.16.8- Exercício 2) Use o Teorema de Stokes para calcular .

é o hemisfério orientado para cima.

(Capítulo 16.7 – Exercício 30) Calcule a integral de superfície para o campo vetorial e superfície orientada . Em outras palavras, determine o fluxo de através de . Para superfícies fechadas, use a orientação positiva (para fora).

é a fronteira da região delimitada pelo cilindro e pelos planos e .

( Cap. 16.7- Exercício 19) Calcule a integral de superfície.

é a parte do cilindro que está entre os planos e no primeiro octante

Use o Teorema de Stokes para calcular

é a metade do elipsoide que se situa à direita do plano orientado na direção do eixo positivo .

Use o teorema de Stokes para calcular . Em cada caso, é orientada no sentido anti-horário quando visto de cima.

, é o triângulo com vértices .

(Capítulo 16.8 – Exercício 8) Use o teorema de Stokes para calcular . Em cada caso, é orientada no sentido anti-horário quando vista de cima.

, é o limite da partes do plano no primeiro octante.

(Capítulo 16.7 – Exercício 31) Calcule a integral de superfície para o campo vetorial e superfície orientada . Em outras palavras, determine o fluxo de através de . Para superfícies fechadas, use a orientação positiva (para fora).

é a fronteira do semicilindro sólido

(Cap.16.8 - Exercício 4) Use o Teorema de Stokes para calcular

(Capítulo 16.8 – Exercício 17) Uma partícula se move ao longo dos segmentos de reta da origem aos pontos e de volta para a origem sob a influência do campo de forças

Encontre o trabalho realizado.

(Capítulo 16.8 – Exercício 10) Use o teorema de Stokes para calcular . Em cada caso, é orientada no sentido anti-horário quando vista de cima.

, C é a curva de intersecção do plano e do cilindro .

(Capítulo 16.8 – Exercício 10) Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial dado e a superfície .

, é a parte do paraboloide que está acima do do plano , com orientação ascendente.

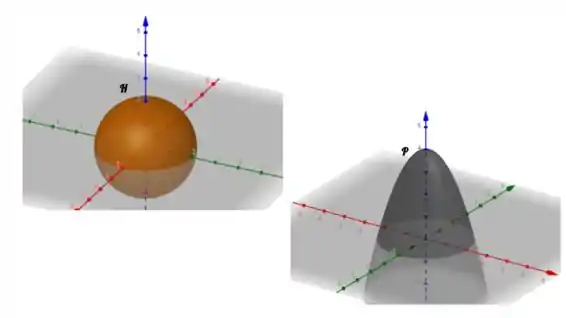
(Cap.16.8 - Exercício 1) Um hemisfério e uma porção de um parabolóide são mostrados. Suponha que seja um campo vetorial sobre cujas componentes tenham derivadas parciais contínuas. Explique por quê

(Capítulo 16.9 – Exercício 5) Use o teorema do divergente para calcular a integral de superfície ; ou seja, calcule o fluxo de através de .

, é a superfície da caixa delimitada pelos planos coordenados e pelos planos , e .

(Capítulo 16.9 – Exercício 7) Use o Teorema do Divergente para calcular a integral de superfície ; ou seja, calcule o fluxo de através de .

, é a superfície do sólido delimitado pelo cilindro e pelos planos e

(Capítulo 16.9 – Exercício 18) Seja . Determine o fluxo de através da parte do paraboloide que está acima do plano e tem orientação descendente.