Listas de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 3 da UTFPR - Sequências e Séries

(Capítulo 11.2 – Exercício 18) Determine se a série é convergente ou divergente. Se for convergente, calcule sua soma.

(Capítulo 11.2 – Exercício 59) Encontre os valores de para os quais a série converge. Calcule a soma da série para esses valores de .

59.

(Capítulo 11.3 – Exercício 4) Use o Teste da Integral para determinar se a série é convergente ou divergente.

4.

(Cap. 11.1. Ex: 7) Liste os cinco primeiros termos da sequência.

(Capítulo 11.2 – Exercício 57) Encontre os valores de para os quais a série converge. Calcule a soma da série para esses valores de .

57.

(Cap. 11.1 – Ex. 12) Liste os cinco primeiros termos da sequência.

(Cap. 11.1 – Ex.48) Determine se a sequência converge ou diverge. Se ela convergir, encontre o limite.

(Cap. 11.2 – Ex. 8) Calcule os oito primeiros termos da sequência de somas parciais corretas para quatro casas decimais. Parece que a série é convergente ou divergente?

(Cap. 11.1 – Ex. 51) Determine se a sequência converge ou diverge. Se ela convergir, encontre o limite.

(Capítulo 11.3 – Exercício 3) Use o Teste da Integral para determinar se a série é convergente ou divergente.

3.

(Cap. 11.1 – Ex.1)

(a) O que é uma sequência?

(b) O que significa dizer que ?

(c) O que significa dizer que ?

(Capítulo 11.3 – Exercício 13) Determine se a série é convergente ou divergente.

(Capítulo 11.3 – Exercício 25) Determine se a série é convergente ou divergente.

(Capítulo 11.3 – Exercício 33) A função zeta de Riemann é definida por

e é usada em teoria de números para estudar a distribuição de números primos. Qual é o domínio de ?

(Capítulo 11.3 – Exercício 24) Determine se a série é convergente ou divergente.

(Capítulo 11.3 – Exercício 26) Determine se a série é convergente ou divergente.

(Capítulo 11.3 – Exercício 29) Encontre os valores de para os quais a série é convergente.

(Capítulo 11.3 – Exercício 17) Determine se a série é convergente ou divergente.

(Capítulo 11.3 – Exercício 5) Use o Teste da Integral para determinar se a série é convergente ou divergente.

(Cap. 11.2 – Ex. 7) Calcule os oito primeiros termos da sequência de somas parciais corretas para quatro casas decimais. Parece que a série é convergente ou divergente?

(Capítulo 11.5 – Exercício 5) Teste a série quanto a convergência ou divergência.

(Capítulo 11.5 – Exercício 6) Teste a série quanto a convergência ou divergência.

(Capítulo 11.4 – Exercício 5) Determine se a série converge ou diverge.

(Capítulo 11.4 – Exercício 17) Determine se a série converge ou diverge.

(Capítulo 11.3 – Exercício 38) Calcule a soma da série com precisão de três casas decimais.

(Capítulo 11.4 – Exercício 31) Determine se a série converge ou diverge.

(Capítulo 11.4 – Exercício 21) Determine se a série converge ou diverge.

(Capítulo 11.4 – Exercício 30) Determine se a série converge ou diverge.

(Capítulo 11.9 – Exercício 3) Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

(Capítulo 11.6 – Exercício 3) Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.

(Capítulo 11.9 – Exercício 7) Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

(Capítulo 11.5 – Exercício 3) Teste a série quanto a convergência ou divergência

(Capítulo 11.6 – Exercício 7) Determine se a serie e absolutamente convergente, condicionalmente convergente ou divergente:

(Capítulo 11.5 – Exercício 7) Teste a série quanto a convergência ou divergência.

Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.

(Capítulo 11.8 – Exercício 18) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.8 – Exercício 15) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.6 – Exercício 4) Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.

(Capítulo 11.5 – Exercício 8) Teste a série quanto a convergência ou divergência.

(Capítulo 11.9 – Exercício 5) Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

(Capítulo 11.8 – Exercício 12) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.8 – Exercício 5) Encontre o raio de convergência e o intervalo de convergência da série.

(Capítulo 11.8 – Exercício 17) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.8 – Exercício 7) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.4 – Exercício 46) Se e forem ambas séries convergentes com termos positivos, é verdade que também será convergente?

(Capítulo 11.5 – Exercício 32) Para quais valores de a serie e convergente?

(Capítulo 11.6 – Exercício 26) Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.

(Capítulo 11.4 – Exercício 29) Determine se a série converge ou diverge.

(Capítulo 11.6 – Exercício 18) Determine se a serie e absolutamente convergente, condicionalmente convergente ou divergente:

(Capítulo 11.8 – Exercício 13) Encontre o raio de convergência e o intervalo de convergência da série:

(Capítulo 11.10 – Exercício 7) Encontre a sére de Maclaurin de f(x) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que ] Também encontre o raio de convergência associado.

(Capítulo 11.9 – Exercício 25) Calcule a integral indefinida como uma série de potências. Qual é o raio de convergência?

(Capítulo 11.9 – Exercício 9) Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

(Capítulo 11.10 – Exercício 9) Encontre a sére de Maclaurin de f(x) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que ] Também encontre o raio de convergência associado.

(Capítulo 11.9 – Exercício 15) Encontre uma representação em série de potências para a função e determine o raio de convergência.

(Capítulo 11.10 – Exercício 8) Encontre a sére de Maclaurin de f(x) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que ] Também encontre o raio de convergência associado.

(Capítulo 11.10 – Exercício 5) Encontre a série de Maclaurin usando a definição de uma série de Maclaurin. [Suponha que tenha expansão em uma série de potências. Não mostre que .] Também encontre o raio de convergência associado.

(Capítulo 11.10 – Exercício 2) O gráfico de é mostrado.

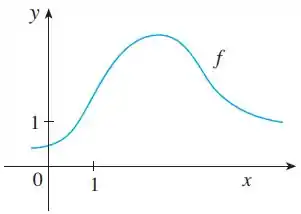
(a) Explique por que a série

não é a série de Taylor de centrada em .

(b) Explique por que a série

não é a série de Taylor de centrada em .

(Capítulo 11.9 – Exercício 17) Encontre uma representação em série de potências para a função e determine o raio de convergência.

(Capítulo 11.10 – Exercício 10) Encontre a série de Maclaurin usando a definição de uma série de Maclaurin. [Suponha que tenha expansão em uma série de potências. Não mostre que .] Também encontre o raio de convergência associado.