Livro James Stewart, Volume 2, 7ª Edição, Capítulo 16, Seção 8, Exercício 8
(Capítulo 16.8 – Exercício 8) Use o teorema de Stokes para calcular . Em cada caso, é orientada no sentido anti-horário quando vista de cima.
, é o limite da partes do plano no primeiro octante.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
O objetivo dessa questão é utilizar o Teorema de Stokes para resolver a integral de linha dada no enunciado. Tá, mas para que serve o Teorema de Stokes?
Stokes criou um teorema que generaliza essa necessidade de calcular as integrais de linha, transformando em uma integral de superfície do rotacional de .
Em termos de equação, é algo mais ou menos assim:
Então, a integral de linha de vira uma integral de superfície do rotacional de . Neste caso,
Agora, partiremos para o cálculo do rotacional do campo :
Em cálculo vetorial, rotacional é um operador que calcula, em uma superfície infinitesimal, o quanto os vetores de um campo vetorial se afastam ou se aproximam de um vetor normal a esta superfície.
E para nos ajudar, consideramos que o rotacional é uma matriz 3x3 que precisamos encontrar uma espécie de determinante com o método de Laplace para a primeira linha.
E aí temos:
Aplicando Laplace na primeira linha:
Desta forma:
Passo 2
Neste caso, a superfície que usaremos na integral de superfície é a parte do plano restrita ao primeito octante. O vetor normal dessa superfície será o vetor normal do plano :
Assim,
Vamos achar os pontos de interseção do plano com os eixos coordenados. Fazendo , achamos
Fazendo , achamos:
E , achamos:
Com esses valores em mente, podemos agora parametrizar a superfície, isolando e deixando e como parâmetros livres:
No plano , temos o seguinte desenho:
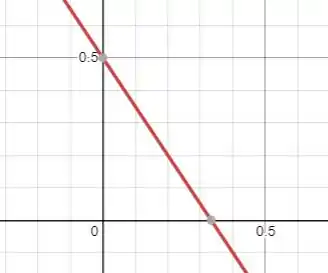
A equação dessa reta é
Assim, a integral de superfície será
Passo 3
Fazendo a primeira integração em :
Vamos rearranjar os termos:
Portanto,
Logo,
Fazendo a integração:
Portanto, pelo Teorema de Stokes:
Prontinho, pessoal! Pra essa questão é isso! Bora resolver mais uma?
