Livro James Stewart, Volume 2, 7ª Edição, Capítulo 16, Seção 8, Exercício 7
Use o teorema de Stokes para calcular . Em cada caso, é orientada no sentido anti-horário quando visto de cima.
, é o triângulo com vértices .
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
O triângulo com vértices em é bem famoso no mundo da matemática.
Ele tem essa carinha aqui:
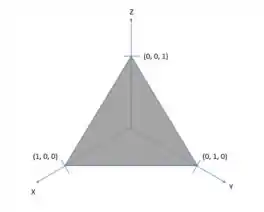
Nesse exercício, precisamos resolver a integral de superfície que está sob o plano formado por esses vértices. Para determinar a superfície , precisamos equacionar esse plano.
Caso esteja com dúvidas sobre a equação do plano, dá uma espiadinha no capítulo para lembrar como é feita a equação de um plano com três pontos. Ok?
A equação desse plano, com vetor normal e ponto (aqui você pode escolher qualquer um dos três pontos para equacionar o plano) vai ser:
Assim .
E o vetor normal a essa superfície vai ser
Passo 2
Legal! O próximo passo é determinar a região de integração. Como é um plano em , os limites vão ser:
E o elemento de área vai ser:
Passo 3
Partiremos para o cálculo do rotacional do campo :
Em cálculo vetorial, rotacional é um operador que calcula, em uma superfície infinitesimal, o quanto os vetores de um campo vetorial se afastam ou se aproximam de um vetor normal a esta superfície.
E para nos ajudar, consideramos que o rotacional é uma matriz 3x3 que precisamos encontrar uma espécie de determinante com o método de Laplace para a primeira linha.
E aí temos:
Aplicando Laplace na primeira linha:
Todos esses valores nos parênteses menores serão derivados pelas variáveis dos denominadores correspondentes.
Aplicando para todos os elementos teremos:
O produto escalar entre e fica:
Passo 4
Agora é colocar tudo na integral:
Prontinho! Pra essa questão é isso, pessoal! Bora resolver mais uma?
